안녕하세요.
이번 장에서는 연속확률분포를 설명하기 위한 여러 개념들에 대해서 살펴보도록 하겠습니다.
확률분포에 대한 개념은 "3-1.이산확률분포"에서 설명했기 때문에 여기에서는 바로 연속확률분포에 대해서 설명하도록 하겠습니다.
1. 연속확률분포를 사용하는 이유
- 앞서 이산확률분포에 대해서 알아보았습니다. 아래 그림을 2000~2024년 동안 비가 얼마나 자주 내렸는지에 대한 현상을 보여주는 데이터라고 해보겠습니다.
- 아래 확률분포를 통해 알 수 있는 사실은 12, 13년도에 비가 제일 자주 내렸다는 것을 알 수 있습니다. 그런데, 12년도 6월에는 얼마나 비가 내렸는지는 알 수 없습니다. 왜냐하면 아래의 정규분포는 연단위가 확률변수(random variable→12년도, 13년도)이기 때문입니다.
- 이처럼 우리는 보통 12년도 1월, 12년도 2월 또는 12년도 1월 1일, 12년도 1월 2일 더 나아가서는 시간대별로 얼마나 비가 내렸는지 알고 싶은 경우가 있습니다. 즉, 이산적인 경우가 아니라 모든 경우를 포함하는 연속적인 데이터(확률변수)에 대한 확률 값을 알고 싶은 경우가 많은 것이죠.

- 그런데, 이러한 모든 연속적인 데이터(=확률변수)를 수집하는 것은 불가능에 가깝습니다. 그렇기 때문에, 데이터(=확률변수)를 수집하고 실험하는 것은 이산적일 수 밖에 없는 것이죠.
- 그렇기 때문에, 이러한 이산적인 데이터(=확률변수→12년도에 내린 비의 횟수, 13년도에 내린 비의 횟수)를 기반으로해서 연속확률변수에 대한 확률 값을 추정하게 됩니다.
- 그럼 지금부터 어떻게 이산적인 데이터를 기반으로 연속확률분포를 그려낼 수 있는지 알아보겠습니다.
2. 이산적인 데이터에서 연속확률분포를 추정하는 법 (Feat. 적분 (구분구적법))
- 먼저, 이산적인 데이터를 설정하는 방식이 이산확률분포에서 봤던 것과 조금 다릅니다.
- 연속확률분포를 추정하기 위해서는 "계급"이라는 개념이 도입됩니다.
- 예를 들어, 몸무게를 확률변수로 삼았다고 해보겠습니다.
- 이산확률분포에서는 몸무게 확률변수가 10,11,12,13 이런식으로 이산적으로 설정이 됩니다. 그렇기 때문에 10.5kg 이라는 확률변수에 대한 확률 값을 알 수 있는 방법은 없는 것이죠.
- 이에 대한 문제를 해결하기 위해, 우리는 10~20 이라는 범위를 설정하고, 해당 범위 안에 들어가는 사람들의 빈도수를 기록합니다. (여기서 중요한 것은 실제로 우리가 얻은 데이터는 10kg, 10.2kg, 14kg 등 일 것이라는 점입니다. 즉, 10.1kg, 10.25kg 이러한 데이터는 없다는 것이죠.)
- 그저 이산적으로 모은 데이터를 10~20라는 범위에 포함시키고 앞선 10.1kg, 10.25kg 과 같은 데이터(=확률변수)에 해당하는 확률 값을 추정하는 것이죠.
- 이 때, 10~20(=A 클래스), 20~30(=B 클래스), 30~40(=C 클래스) 등 이런식으로 계급을 통해 표현하는 것이 연속확률변수를 추정하는 핵심 포인트가 됩니다. (어디까지나 이산적인 데이터를 계급안에 포함시켜 연속확률변수에 대한 확률 값을 추정하는 것이지, 추정된 확률변수가 해당 확률 값 만큼 실제세계에서 존재하는지는 알 수 없습니다)
- 예를 들어, 몸무게를 확률변수로 삼았다고 해보겠습니다.
- 그렇다면, 앞서 언급한 과정들이 어떻게 진행되면서 연속확률분포를 추정할 수 있는지 알아보겠습니다.

↓↓↓Normalization 설명↓↓↓
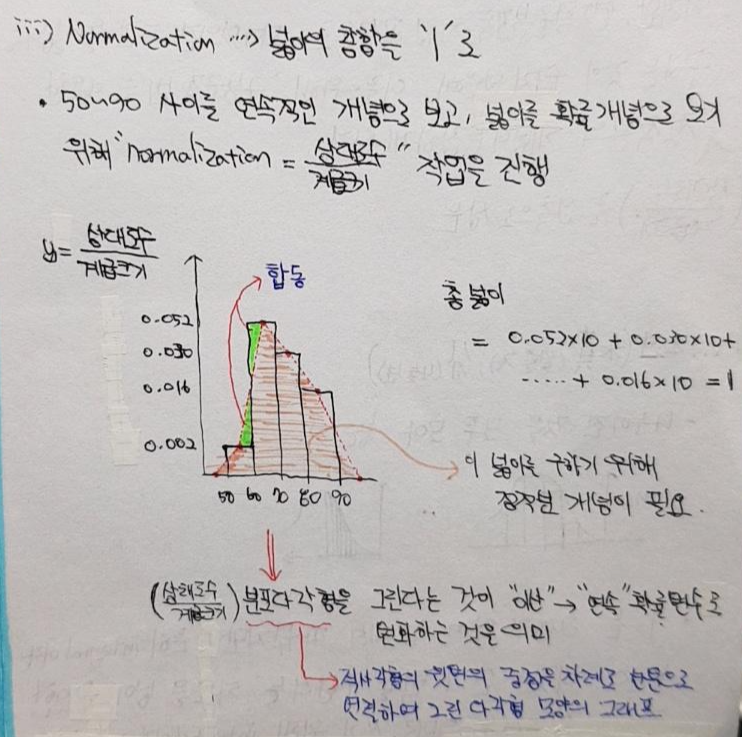

↓↓↓구분구적법↓↓↓
https://www.youtube.com/watch?v=7vcHY2a4154
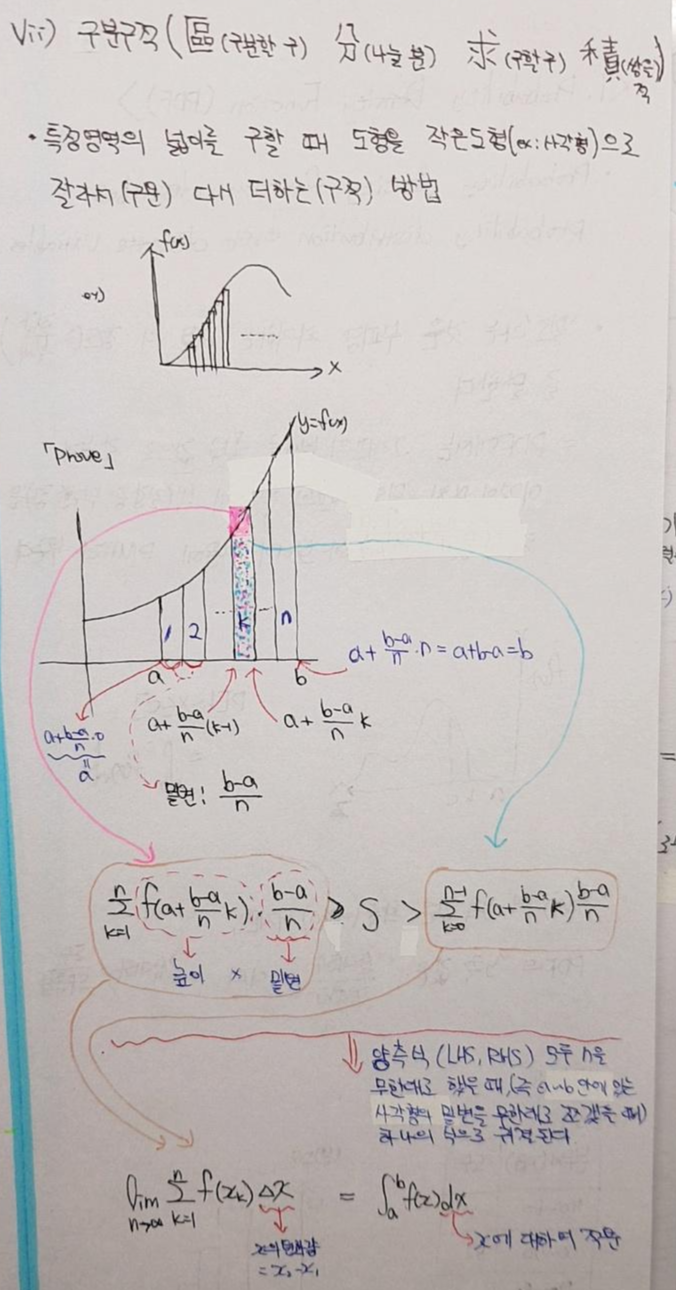
- 결국 연속확률분포에서의 확률 함수(P(x))는 확률분포로 나타내는 그래프 상의 면적이 됩니다. 이에 대한 자세한 설명은 바로 뒤에서 설명하도록 하겠습니다.
3. Probability Density Function (PDF) with 3가지 axiom
- PDF는 간단히 말해 확률 함수(→ 확률함수 설명 링크)가 취하는 정의역이 연속확률변수(continuous probability variable)일 뿐입니다 (→확률변수 설명 링크).
- Probability density function describes a probability distribution over continuous variables.
- 앞서 언급한 계급이라는 개념이 도입이되면서 연속확률변수를 고려하는 확률분포을 수 있게 됐습니다.
- PDF는 확률함수이므로 P(X)라고 표현합니다. 여기 중요하게 봐야할 것은 이산확률분포에서 y축이 확률 값을 의미한 반면, 연속확률 분포에서의 y축은 확률 값을 의미하지 않습니다. 연속확률분포에서는 '면적'이 확률 값이 기 때문에 f(x)≠p(x) 인 셈이되는 것이죠.
- 그렇기 때문에 정확히 확률함수(P(X))는 아래와 같이 표현하게 됩니다.


- 하지만, 우리는 f(x)를 확률밀도함수(PDF)라고 부릅니다. 왜냐하면, f(x)는 확률변수의 분포를 표현해주기 때문이죠 (사실 f(x)값 자체가 확률 값을 도출하는 건 아니라 확률(밀도)함수라고 붙이는게 좋은게 이해가 되진 않네요....).
- 그리고, f(x)를 특정 구간으로 적분해주면 확률 값을 구할 수 있는데, 이 때 \(\int_{a}^{b}{f(x)}\)는 누적분포함수(CDF)라고 합니다 (누적분포함수는 "3-2. 이산확률 분포 종류들"를 참고해주세요)
- 예를 들어, 아래 정규분포의 확률밀도함수 f(x)는 아래 그림에서 나타내는 수식을 따르고, 해당 확률함수는 누적분포함수인 f(x)의 적분식으로 표현합니다.


- 연속확률함수에는 3가지 공리가 있습니다.
③먼저, 세 번째 공리는 위에서 설명한 연속확률분포에서의 확률함수와 관련된 부분입니다.

①첫 번째는 이산확률함수와 마찬가지로 모든 확률변수의 확률 값을 다 더했을 때 총합이 1이 되어야 한다는 점입니다.
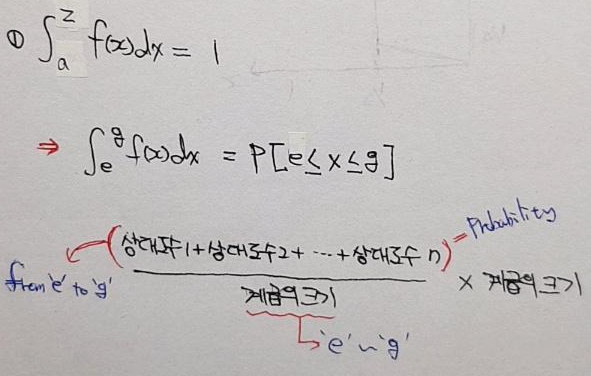
② 두 번째는 연속확률분포서 y축을 담당하는 f(x) 부분이 1보다 클 수 있다는 접입니다. 이산확률분포에서 y축은 f(x)=p(x) 였기 때문에, f(x) 값의 제한범위는 "0≤f(x)≤1"인 반면에, 연속확률분포에서 f(x)는 p(x)가 아니기 때문에, "≤1"에 대한 제한이 없어지는 것이지요.

4. 연속확률분포의 평균과 분산
- 연속확률분포의 평균과 분산은 이산확률 분포의 평균과 분산과 동일한 맥락입니다. 연속확률분포에서는 확률변수가 연속적이기 때문에 이를 고려해 "(연속)확률함수와 해당 확률변수간의 관계식"으로 나타내면 됩니다. (참고로 연속확률분포에서의 x는 범위를 갖는다는 점을 염두해두시면 좋을 것 같습니다.)

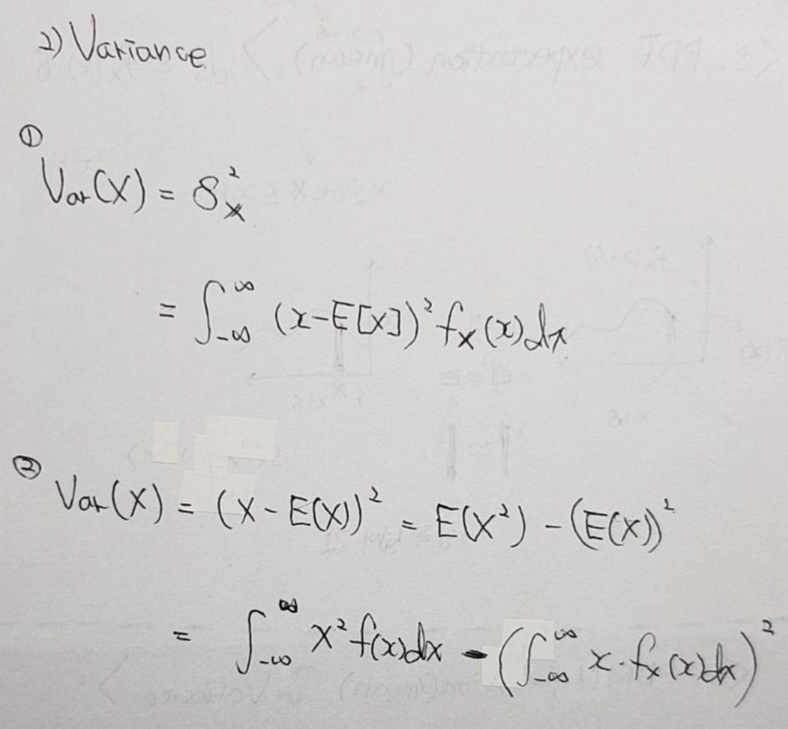
지금까지 연속확률분포의 개념과 그와 관련된 여러 개념들(평균, 분산 등)에 대해서 알아보았습니다.
다음 글에서부터는 여러가지 연속확률분포 종류들에 대해서 알아보도록 하겠습니다.