안녕하세요~
이번 장에서는 확률의 개념과 관련된 전반적인 용어 설명들을 하도록 하겠습니다.
1. 확률의 기원
확률이라는 학문은 도박을 그 기원으로 두고 있는데요. 이에 대한 설명이 담긴 영상을 보도록 하겠습니다.
https://www.youtube.com/watch?v=F8TMnn8SW4c
2. 확률의 사전적 의미
- 확률의 한자 뜻은 다음과 같습니다.
- 확실할 "확" + 비율 "율" = 확실함의 비율(정도)
- 다음은 영어에서 정의하는 확률의 뜻을 살펴보도록 하겠습니다.
- Probability is the measure of the likelihood(=%) that an event in sample space will occur.
- 여러 해석이 가능하겠지만 위의 두 설명을 한 단어로 설명하자면 '가능성의 정도'라고 할 수 있겠네요. 당연히 수학분야에서 사용되기 때문에 '정도'를 수치로 표현할 것이구요.
- 가능성이라는 것이 갖는 특징은 어떤 행위가 비결정적인 결과를 낳을 때 사용 가능한 용어라는 점입니다.
- 비결정적 결과: 주사위를 던지는 행위
- 결정적 결과: 물리법칙 → \(E=mc^2 \)
3. 수학적 확률(가능성) = 라플라스 확률
- 위에서 정의한 사전적 정의를 좀 더 구체적으로 표현하면 아래와 같습니다.
- 확률실험(시행: trial)을 통해 얻은 모든 실험결과(표본공간: Sample space)들 중에서 특정사건(event)이 일어나는 것에 대한 확신(믿음)의 정도(가능성: probability)를 의미 → 어떤 사건(event)이 일어날 가능성을 수치로 나타낸 것
- 용어1. 확률실험 (시행: trial): 우연의 요소(비결정적 결과→아래에서 설명)를 포함하는 실험으로써 아래 두 가지를 만족하는 실험
- 1. 같은 조건에서 반복시행이 가능한 실험
- 2. 매 실행 결과가 무엇이 될지는 알 수 없으나, 실현 가능한 모든 결과들을 시행전에 알 수 있는 실험
- 3. ex) 주사위 확률시험
- 용어2. Sample space=표본공간 (Ω,s)
- Sample space는 확률실험(trial)에서 실현 가능한 모든 결과를 원소(element)로 갖는 집합(set)이다.
- ex) 주사위 던지는 실험에서의 표본 공간 Ω = {1,2,3,4,5,6}
- 용어3. Event (사건) = 어떤 시행의 특정한 결과 (표본 공간의 부분집합을 의미)
- ex) 주사위를 두 번 던졌을 때, "2,4"가 나왔다면 → E = {2,4}
- 용어1. 확률실험 (시행: trial): 우연의 요소(비결정적 결과→아래에서 설명)를 포함하는 실험으로써 아래 두 가지를 만족하는 실험
- 확률실험(시행: trial)을 통해 얻은 모든 실험결과(표본공간: Sample space)들 중에서 특정사건(event)이 일어나는 것에 대한 확신(믿음)의 정도(가능성: probability)를 의미 → 어떤 사건(event)이 일어날 가능성을 수치로 나타낸 것
- 위와 같은 정의하에 A사건이 나타날 확률을 표현하는 수학적 확률의 정의는 아래와 같습니다.
- A의 수학적 확률 = P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{사건 A의 원소 개수}{표본공간의 원소 개수}\) = \(\frac{사건 A가 나타나는 경우의 수}{전체의 경우의 수}\)
- 고등학교때 확률을 배우기 전에 경우의 수를 왜 배우는지 아시겠죠? 아래 목록들은 중고등학교 교과과정에서 배우는 경우의 수 인데,여기에서는 몇몇 부분만 뒷 부분에서 다루도록 하겠습니다.
- 합의법칙과 곱의법칙
- 순열, 원순열, 같은 것을 포함하는 순열, 최단 경로의 수, 중복순열
- 조합, 도형의 개수, 중복조합
- 분할, 색칠문제, 좌석배치, 숫자 만들기, 이항정리, 이항계수의 성질
4. 확률의 기본 두 가지 이론
- 확률의 근간을 이루는 이론 중에 가장 기본이 되는 두 가지 확률이론 있습니다.
- 두 사건의 합집합 (A라는 사건이 일어나거나, B사건이 일어날 경우) 에 대한 확률→ 확률의 덧셈정리
- 두 사건의 교집합 (A, B 사건이 동시에 일어날 경우 OR A 사건이 일어나고, 연속해서 B 사건이 일어날 경우) 에 대한 확률 → 확률의 곱셈정리
- 지금부터 이 두 가지 이론에 대해서 알아보도록 하겠습니다.
4-1. 덧셈정리(Addition theorem of probability) with 배반사건(Exclusive evnet)
- A라는 사건이 일어나거나(OR) B라는 사건이 일어날 경우의 확률을 구할 때
- \(\frac{n(A\cup B)}{n(S)}\) = \(\frac{n(A)}{n(S)}\) + \(\frac{n(B)}{n(S)}\) - \(\frac{n(A\cap B)}{n(S)}\)
- \(P(A\cup B) = P(A) + P(B) - P(A\cap B)\)
- 덧셈정리과 관련해서 알아두어야 할 한 가지 개념이 있습니다.
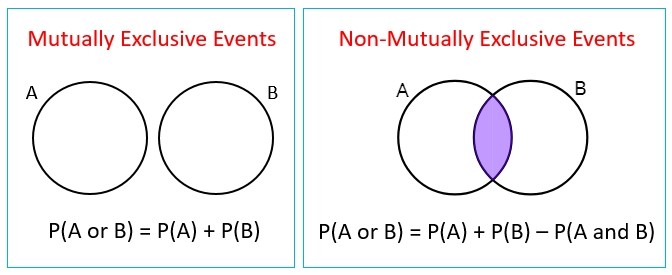
- 배반사건(Exclusive Event)
- 우리가 A라는 사건이 일어나거나 B라는 사건이 일어날 확률을 구한다고 했을 때, A라는 사건과 B라는 사건이 동시에 일어나지 않을 수도 있습니다. 이름 그대로 두 사건이 접점이 없이 서로 배타적임을 의미합니다. 그리고, 이러한 개념을 수학적으로 표현하면 다음과 같습니다. → \(P(A\cap B) = 0\)
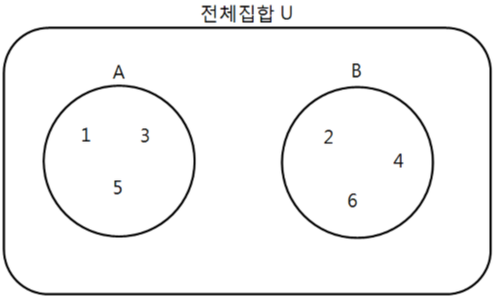
- ex) 주사위를 던졌을 때 홀수가 나오거나 (=A사건), 짝수가 나올(=B사건) 경우 A, B 사건을 배반 사건이라 할 수 있습니다.
- 그래서 A와 B가 서로 배반사건인 상황에서의 덧셈정리는 다음과 같이 정리할 수 있습니다.
- \(P(A\cup B) = P(A) + P(B)\)
- 배반사건(Exclusive Event)
4-2. 곱셈정리(Multiply theorem of probability) with 종속사건(Dependent event), 독립사건(Independent event), 조건부확률(Conditional probability)
- 확률엥서 곱셈을 하는 경우는 A와 B사건이 동시에 일어날 경우입니다.
- 또한, 확률 곱셈은 A라는 사건이 일어나고 연속적(순차적)으로 B라는 사건이 일어날 확률을 구할 때도 사용합니다.
- 예를 들어, 아래 그림과 같이 서울에서 대전으로 갈 때 1, 2, 3 맛집이 있고, 대전에서 부산으로 갈때 4, 5라는 맛집이 있다고 하겠습니다. 아침은 A 맛집에서 먹고 점심은 D 맛집에서 먹을 수 있는 확률은 어떻게 될까요?

- 확률의 곱셈정리와 관련해서 알아야할 개념이 있습니다.
- 위에서 설명한 곱셈정리는 독립사건을 가정하고 있습니다. 그렇다면 독립사건은 무엇일까요?
- 독립사건을 알아보기 전에 종속사건을 먼저 살펴보겠습니다, 종속사건을 설명하려면 조건부 확률을 알고 있어야 하니 "조건부확률 → 종속사건 → 독립사건" 순서로 글을 정리해보도록 하겠습니다.
4-2-1. 곱셈정리(Multiply theorem of probability) with 종속사건(Dependent event), 독립사건(Independent event), 조건부확률(Conditional probability)
- 확률 곱셈을 이용하여 독립사건, 종속사건, 조건부확률을 알아보도록 하겠습니다
- 용어1. 조건부확률: B라는 사건이 주어졌을 때 A사건이 일어날 확률
- Probability of A, Given that B occured
- P(B|A)
- 아래 영상에서 조건부 확률과 관련된 재미난 영상을 한 번 확인해보셔도 좋을 것 같습니다.
- 용어1. 조건부확률: B라는 사건이 주어졌을 때 A사건이 일어날 확률
https://www.youtube.com/watch?v=5DSYQx0iL7I
-
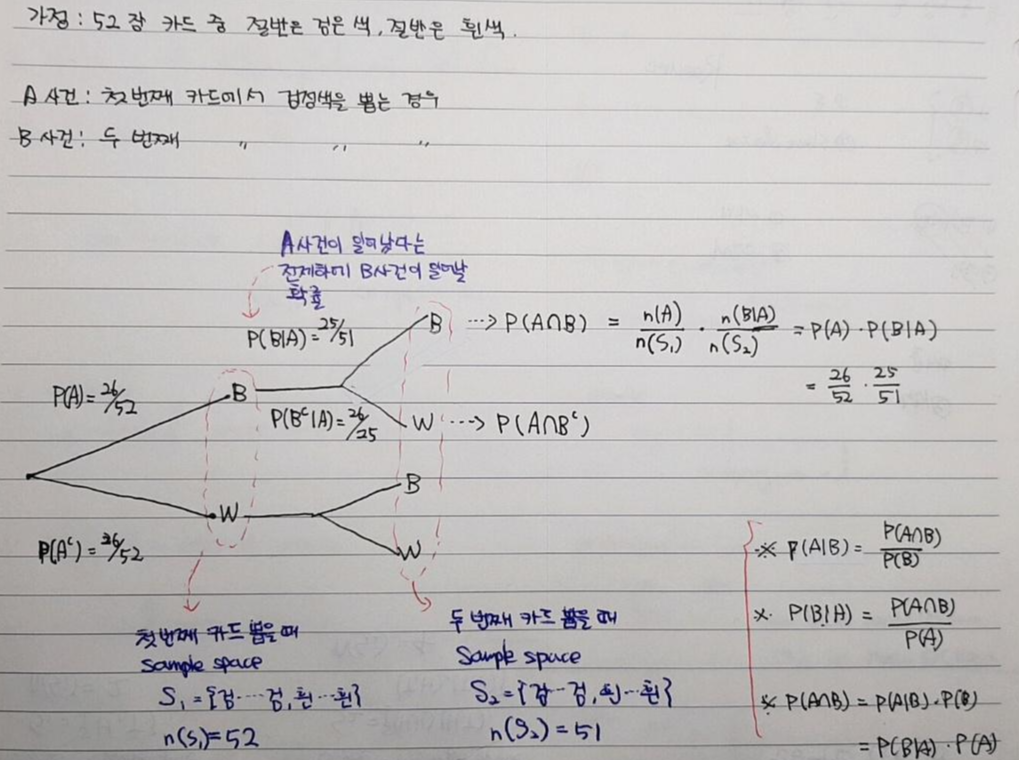
- 용어2. 종속사건: A라는 사건이 B라는 사건에 영향을 줄 때 → 즉, 두 사건이 일어나는 순서에 따라 서로 영향을 주고 받을 때, A와 B는 종속사건이라고 합니다.
- 예를 들어, 52장의 카드를 첫 번째 뽑은 (A사건) 결과가, 두 번째 뽑을 경우의 (B사건) 에 영향을 미치는 경우 → ex) A사건의 표본공간 = 52, B사건의 표본공간 = 51
- 용어2. 종속사건: A라는 사건이 B라는 사건에 영향을 줄 때 → 즉, 두 사건이 일어나는 순서에 따라 서로 영향을 주고 받을 때, A와 B는 종속사건이라고 합니다.
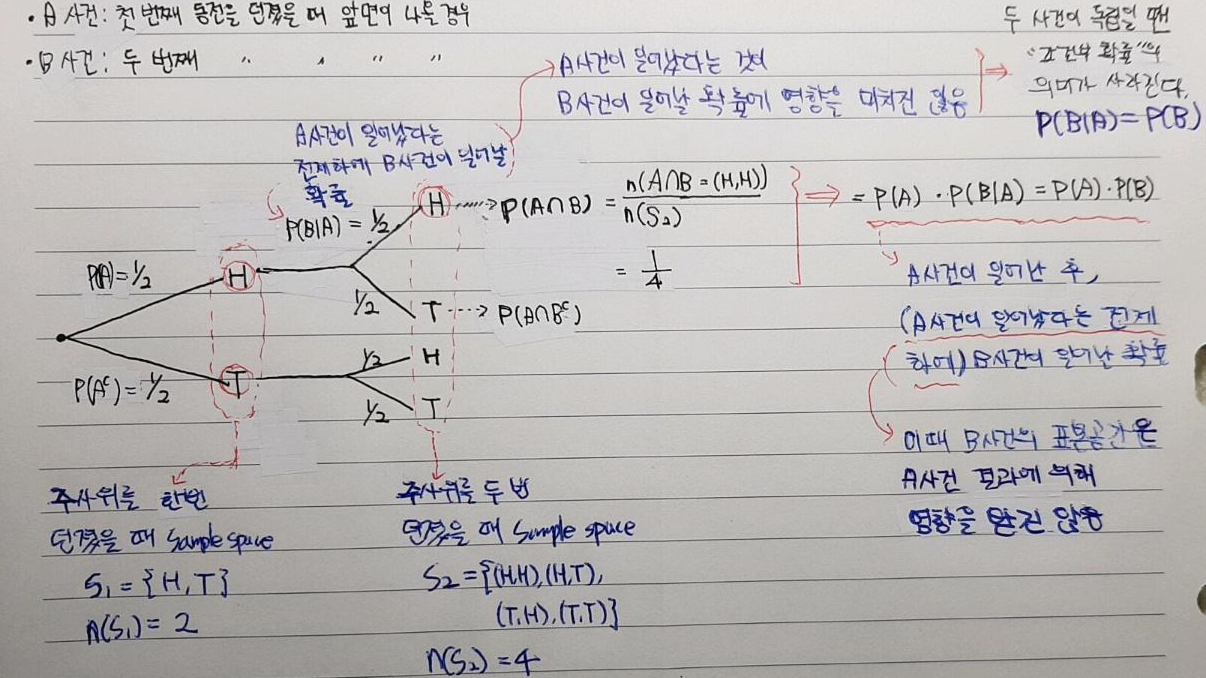
- 용어3. 독립사건: A라는 사건이 B라는 사건에 영향을 주지 않을 때 → 즉 두 사건이 서로 관계가 없이 독립적일 때
- 예를 들어, 첫 번째 주사위를 던졌을 때 앞면이 나왔다고 했을 때 (A사건), 두 번째 주사위를 던졌을 때 앞면이 나올 결과에 (B사건) 어떠한 영향도 미치지 않음

5. 독립시행 확률 (베르누이 확률, Binomial Probability) with 순열(Permutation), 조합(Combination)
- 앞서 독립사건에 대해서 알아보았습니다.
- 그렇다면, 독립사건인 상황(조건)에서 사용할 수 있는 확률 개념인 '독립시행 확률'에 대해서 알아보도록 하겠습니다.
- 우선, 독립시행 확률을 이해하기 위해 순열, 조합에 대한 개념부터 알아보겠습니다.
5-1. 순열
- 순서를 고려하여 나열한 경우의 수 (= 줄 세우는 방법의 수 = 자리 바꿈하는 방법의 수)
- n명에서 r명을 뽑아 줄 세우는 방법의 수 = \(_{n}P_{r}\) = \(\frac{n!}{(n-r)!}\)
- ex) "철수, 영희, 민정, 현진, 정태"가 A, B, C 에 앉을 수 있는 경우의 수는?순열

5-2. 조합 (Combination)
- 순서에 상관없이 구성원을 뽑기만 하는 경우
- n명에서 r명을 뽑는 경우의 수 = \(_{n}C_{r}\) = \(\frac{n!}{(n-r)!r!}\) = \(_{n}C_{n-r}\)
- 순열을 또 다른 관점에서 보면 크게 두 가지 action으로 분류할 수 있습니다
- \(_{5}P_{3}\) → 5명 중 3명을 선택하는 경우의 수 × 뽑힌 3명을 일렬로 나열 하는 수 = \(_{5}C_{3}\)×3!
- 이러한 관점으로부터 조합 공식을 유도할 수 도 있음
5-3. 독립시행 확률(베르누이 확률, Binomial probability)
- 우리 인생에서 알고 싶은 확률들이 보통은 성공 또는 실패할 확률입니다.
- 이러한 조건에서 공(나온)에 대한 확률이 고정되어 있다고 가정해보겠습니다.
- 이때 고정된 성공 또는 실패의 확률을 갖고 있는 독립인 사건을 여러 번 시행했을 때 얻은 확률을 독립시행 확률이라 합니다.
- \(_{시행횟수}C_{성공횟수}\)×\(성공확률^{성공횟수}\)×\(실패확률^{실패횟수}\)
- 시행횟수=n, 성공횟수=r, 실패횟수=k, 성공확률=p, 실패확률=p-1 이라고 했을 때
- \(_{n}C_{r}\)×\(p^{r}\)×\((p-1)^{k}\)

6. 전체 확률의 법칙 = 전확률 정리 (Law of Total Probability)
- 전확률 정리는 조건부 확률 (Conditional probability) 로부터 조건이 붙지 않는 확률 (Unconditional probability) 을 계산 할 때 쓸 수 있습니다.
- When we face a complicated problem, sometimes, it gives us simple solution that the complicated problem is broken up simpler pieces. → 베이즈 정리에서 전확률 정리를 이용함 (바로 뒷 부분에서 베이즈 정리 설명)

7. 베이즈 정리
- 우리가 현재 어떤 사건 A에 대학 사전 확률(prior knowledge)을 알고 있다고 하겠습니다.
- 사전 확률은 말그대로 지금까지의 경험을 바탕으로 설정된 A사건에 대한 확률 값입니다.
- 즉, 앞으로의 경험(데이터)에 따라 A사건에 대한 확률 값은 변경(updating)될 수 있습니다.
- 즉, 우리는 이전에 갖고 있었던 사건A에 대한 우리의 믿음의 정도 (사전확률)를 새로 경험하여 얻는 정보(data)에 따라 updating을 해야, 사건A에 대한 확률 값이 점점 신뢰성을 갖게 될 것입니다.
- 정리하자면, 새로운 정보를 얻었을 때 베이즈 정리를 이용해 해당 사건에 대한 최신 확률 값을 얻을 수 있습니다.
- 예시
- H라는 사건이 일어날 확률 = P(H)
- H라는 사건이 참이라는 조건하에 D가 일어날 수 있는 확률 = P(D|H)
- D라는 데이터가 주어졌을 때 H가 일어날 확률 = P(H|D) = \(\frac{P(H\cap D)}{P(D)}\) = \(\frac{P(H)P(D|H)}{P(D)}\)
- 분모가 되는 P(D) 부분을 전확률 정리로 풀어 쓸 수 있다 → 자세한 것은 문제를 통해 설명





8. 통계적 확률
- 주사위를 한 번 던졌을 때 1이 나올 확률이 6이라고 알고 있습니다. 다시말해, 주사위를 6번 던져야 1이 한 번 나올 것이라는 말과 같다고 할 수 있습니다.
- 하지만 현실에서는 주사위를 6번 던져도 1이 나올 확률이 1/6이 안될 수 도 있습니다.
- 여기에서는 주사위를 6번 던졌으니 시행횟수가 6입니다. 그런데, 이 시행횟수를 한 없이 늘리다보면 결국 1이 나올 확률이 우리가 알고 있는 수학적 확률인 1/6에 근사하게 됩니다.
- 즉, 어떤 시행(trial)을 여러 번 반복했을 때 \(\frac{나온횟수}{시행횟수}\) 는 시행횟수가 한 없이 커짐에 따라 특정한 값에 가까워지는데, 이를 통계적 확률이라 합니다. ex) 타율
- 실제로는 시행 횟수를 한 없이 커지게 할 수 없으므로 시행횟수가 충분히 클 때의 값을 통계적 확률로 봅니다.
- 결과적으로, 시행횟수가 커지다보면 결국 통계적 확률이 수학적 확률에 가까워진다는 철학이 깔려있습니다.
지금까지 확률에 대한 개념과 관련된 전반적인 개념을 다루었습니다. 다음 장에서는 확률분포라는 개념을 이해해보도록 하겠습니다.
[정리]
1. 확률은 "확률실험(시행: trial)을 통해 얻은 모든 실험결과(표본공간: Sample space)들 중에서 특정사건(event)이 일어나는 것에 대한 확신(믿음)의 정도(가능성: probability)를 의미" → 어떤 사건(event)이 일어날 가능성을 수치로 나타낸 것
- A의 수학적 확률 = P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{사건 A의 원소 개수}{표본공간의 원소 개수}\) = \(\frac{사건 A가 나타나는 경우의 수}{전체의 경우의 수}\)
2. 확률에는 두 가지 기초연산이 있다.
2-1. 덧셈정리(Addition theorem of probability) with 배반사건(Exclusive event)
- 확률에서 덧셈이 사용되는 경우: A라는 사건이 일어나거나(OR) B라는 사건이 일어날 경우의 확률을 구할 때
- \(\frac{n(A\cup B)}{n(S)}\) = \(\frac{n(A)}{n(S)}\) + \(\frac{n(B)}{n(S)}\) - \(\frac{n(A\cap B)}{n(S)}\)
- \(P(A\cup B) = P(A) + P(B) - P(A\cap B)\)
- 배반사건(Exclusive Event) = \(P(A\cap B) = 0\)
2-2. 곱셈정리((Multiply theorem of probability) with 종속사건(Dependent event), 독립사건(Independent event), 조건부확률(Conditional probability))
- 확률에서 곱셈이 적용되는 경우: A라는 사건이 일어나고 연속적(순차적)으로 B라는 사건이 일어날 확률을 구할 때 사용한다.
- 어떤 사건이 연속적으로 일어날 때 이전 사건이 다음 사건에 영향을 미치는 경우에 필요한 개념 및 수식
- 종속사건(Dependent event)
- \(P(A\cap B)\) = P(B|A)P(A) = P(A|B)P(B)
- 조건부 확률 (Conditional Probability): P(B|A) -> A라는 사건이 발생했을 때 B라는 사건이 발생할 확률
- 어떤 사건이 연속적으로 일어날 때 이전 사건이 다음 사건에 영향을 미치지 않는 경우에 필요한 개념 및 수식
- \(P(A\cap B)\) = P(A)P(B)
- 독립사건(Independent event) → P(B|A) = P(B)
3. 독립시행 확률 (베르누이 확률, Binomial probability)
- 고정된 성공 또는 실패의 확률을 갖고 있는 독립인 사건을 여러 번 시행했을 때 얻은 확률을 독립시행 확률이라 한다.
- 시행횟수=n, 성공횟수=r, 실패횟수=k, 성공확률=p, 실패확률=p-1 이라고 했을 때
- \(_{n}C_{r}\)×\(p^{r}\)×\((p-1)^{k}\)

4. 베이즈 정리 with 전확률 정리
- 이전에 갖고 있었던 사건A에 대한 우리의 믿음의 정도 (사전확률)를 새로 경험하여 얻는 정보(data)에 따라 updating할 수 있다.
- 즉, 새로운 정보를 통해 얻은 한 사건A에 대한 최신 확률 값을 베이즈 정리를 통해 얻을 수 있다.
- D라는 데이터가 주어졌을 때 H가 일어날 확률 = P(H|D) = \(\frac{P(H\cap D)}{P(D)}\) = \(\frac{P(H)P(D|H)}{P(D)}\)
