안녕하세요.
이번 글에서는 contrastive learning에 대해서 설명하도록 하겠습니다.
Contrast라는 용어를 정의하면 아래와 같습니다.
"A contrast is a great difference between two or more things which is clear when you compare them."
그렇다면, contrastive learning이라는 것은 대상들의 차이를 좀 더 명확하게 보여줄 수 있도록 학습 한다는 뜻이 되겠죠?
'대상들의 차이'라는 말에서 중점적으로 봐야 할 것은 '차이'라는 용어입니다. 보통 어떤 '기준'으로 인해 '차이'가 발생합니다.
예를 들어, 어떤 이미지들이 서로 유사하다고 판단하게 하기 위해서는 어떤 기준들이 적용되어야 할까요? 즉, 어떤 '기준'을 적용하면 이미지들이 비슷한지, 비슷하지 않은지에 대한 '차이'를 만들어 낼 수 있을까요?
고양이라는 이미지가 있다고 가정해보겠습니다. 고양이 이미지에 augmentation을 주게 되도 그 이미지는 고양이 일 것입니다. 즉, 원본 고양이 이미지와 augmentation이 적용된 고양이 이미지는 서로 유사(=positive pair)하다고 할 수 있죠.

누군가(제3자)가 augmented image에 굳이 'similar'라고 labeling 해줄 필요 없이 input data 자기 자신(self)에 의해 파생된 라벨링(supervised ← ex: augmented image) 데이터로 학습(learning)하기 때문에 self-supervlsed learning이라고 할 수 있습니다.
"하지만 'similar' 정의는 어떤 기준을 삼느냐에 따라 굉장히 달라 질 수 있습니다."
물론, similar를 찾는 방법도 굉장히 다양하겠죠. 지금부터 이에 대해서 천천히 알아보도록 하겠습니다.
1. Similarity learning
앞서 언급한 내용 중에 가장 핵심적이고 자주 등장하는 용어가 'similar'입니다. 그렇다면, contrastive learning과 similarity learning은 어떤 관계가 있을까요? 먼저, similarity learning의 정의부터 살펴보겠습니다.
"Similarity learning is closely related to regression and classification, but the goal is to learn a similarity function that measures how similar or related two objects are."
결국, contrastive learning과 similarity learning 모두 다 어떤 객체들에 대한 유사도와 관련이 있다는걸 알 수 있습니다.

좀 더 similarity learning을 알아볼까요?
먼저, similarity learning의 3가지 종류들에 대해서 알아보도록 하겠습니다.
(↓↓↓참고 자료↓↓↓)
https://en.wikipedia.org/wiki/Similarity_learning
Similarity learning - Wikipedia
Similarity learning is an area of supervised machine learning in artificial intelligence. It is closely related to regression and classification, but the goal is to learn a similarity function that measures how similar or related two objects are. It has ap
en.wikipedia.org
1-1. Regression similarity learning

- 두 객체(ex: 이미지)간의 유사도를 알고 있다는 전제하에 supervised learning 학습을 시키는 것
- 유사도는 어떤 기준(pre-defined)에 의해 설정되는데, 이 기준에 의해 모델이 학습됨
- 위의 y가 유사도를 나타내 주는 값 → 즉, 유사도가 높으면 y 값이 높게 설정 됨
- 앞서 설정한 유사도에 따라 모델이 학습되면, 학습된 모델에 test 데이터인 두 객체(ex:이미지)가 입력 될 때 pre-defined 기준에 따라 유사도를 결정
- Ex) 강아지 이미지 데이터들 간에는 모두 강한 유사도를 주고, 강아지 이미지 데이터와 고양이 이미지 데이터들의 유사도는 굉장히 낮은 값으로 설정해주어 학습 시키면, 학습 한 모델은 강아지 이미지들끼리에 대해서 높은 유사도 값을 regression할 것 입니다.
- 하지만, 이러한 유사도(y)를 미리 알고 어떻게 할당해줄 것인지는 굉장히 어려운 문제
1-2. Classification similarity learning

[앞선 "Regression similarity learning" 방식과 다른 점]
- Regression: y∈R
- 유사도(=y) 값의 범위는 실수 (ex: 0~1) → 유사도의 정도를 파악할 수 있음
- 이때, R값의 범위를 어떻게 설정하고, 어떤 y값을 해줘야 하는지 어려움 (soften label 개념정도로 봐도 될 듯)
- Classification: y ∈{0,1}
- 두 객체가 유사한지 아닌지만 알려주기 때문에 입력으로 들어오는 두 객체(ex:이미지)가 어느 정도로 유사한지는 알 수 없음
1-3. Ranking similarity learning

[앞선 두 가지 방식("regression or classification similarity learning")과 다른 점]
- 앞선 두 가지 방식과 다른 부분은 "세 가지 입력 데이터 (triplets of objects)"를 필요로 한다는 점입니다.
- 일반적인 데이터 "x"와 "x와 유사한 x+", "x와 유사하지 않은 x-" 데이터가 입력으로 들어갑니다.
- 이런식으로 유사한 데이터들 간의 유사도와 유사하지 않은 데이터들 간의 유사도 차이를 위와 같이 설정하여 학습하게 됩니다.
결국 contrastive learning과 similarity learning 모두 데이터들 간의 similarity를 알아내는 것이 목적입니다.
"Contrastive learning is an approach to formulate the task of finding similar and dissimilar things for an ML model."

"Similarity learning is closely related to distance metric learning."
데이터들끼리 유사도가 높다는 것을 거리(distance)의 관점에서 해석해볼 수 도 있습니다. 예를 들어, 유사한 데이터 끼리는 거리가 가깝다는 식으로 해석해 볼 수 있는 것이죠. 그래서, similarity learning, contrastive learning을 배우다 보면 distance metric learning이라는 용어가 자주 등장합니다.
2. (Distance) Metric learning
유사도를 판단하는데 있어서는 굉장히 다양한 기준이 적용될 수 있습니다. 유사도를 판단하는 한 가지 방법은 거리의 관점에서 해석하는 것입니다.
보통 거리라는 개념을 단순히 점과 점 사이의 최단 거리로만 이해하는 경우가 있지만, 거리를 측정하는 방식에는 다양한 방법이 존재 합니다. 즉, "거리"라는 개념을 어떻게 해석하느냐가 굉장히 중요한 문제라고 볼 수 있습니다.
결국, 두 객체간의 거리를 측정할 수 있는 방법이 다양하기 때문에 두 객체간의 유사도를 적용할 수 있는 기준이 다양하다고 할 수 있습니다.
"Similarity learning is closely related to distance metric learning. Metric learning is the task of learning a distance function over objects."
위의 정의에 따라 metric learning은 객체간의 거리를 학습하는 방법들에 대해 연구하는 분야라고 할 수 있습니다.
그렇다면, metric이라는 개념부터 정의해볼까요?
"A Metric is a function that quantifies a “distance” between every pair of elements in a set, thus inducing a measure of similarity."
객체(데이터)들 간의 거리(or 유사도)를 수량화 하는 방법은 여러가지가 있습니다. (결국, 우리가 배우는 contrastive learning 기법에서도 아래와 같은 metric들 중에 어느 것을 사용하느냐에 따라 다양한 연구가 진행 될 수 있겠죠.)

Metric learning에서 중요한 개념은 '거리'입니다. 그렇기 때문에, metric learning에서 정의한 4가지 속성도 '거리'의 속성을 그대로 반영하고 있죠.
"A metric or distance function must obey four axioms"
- Non-negativity: f(x,y)≥0
- x, y 두 데이터 간의 거리는 음수가 될 수 없다.
- Identity of Discernible: f(x,y)=0 <=> x=y
- x, y 두 데이터 간의 거리가 0이라면, x와 y 데이터는 동일하다.
- Symmetry: f(x,y) = f(y,x)
- "x,y" 간의 거리나, "y,x" 간의 거리는 같다
- Triangle Inequality: f(x,z)≤f(x,y)+f(y,z)
- "x,z"간의 거리는 "x,y" 간의 거리와 "y,z"간의 거리를 합한 것보다 클 수 없다.
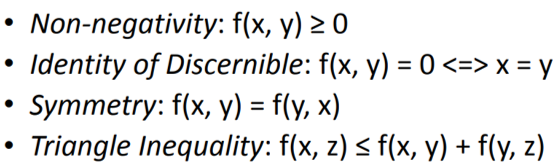
2-1. Metric of Two types
거리를 측정하는 metric 방식에도 크게 두 가지 종류가 있습니다.
- Pre-defined Metrics
- 단순히 데이터들을 정의 된 metric 공식에 입력하고 '거리' 값을 도출하여 유사도 비교
- Learned metrics
- 데이터들로 부터 추정할 수 있는 다른 지표들을 metric 공식에 적용하여 '거리' 값을 도출

'Learned metrics' 방식의 대표주자라고 할 수 있는 것은 딥러닝을 이용한 deep metric learning 방식입니다. 그럼 지금부터 deep metric learning에 대해 좀 더 알아보도록 하겠습니다.
2-2. Deep Metric Learning (Feat. Contrastive loss)
객체(데이터)들이 만약 고차원이라면 서로 간의 유사도를 비교하는건 굉장히 어려운 문제가 될 수 있습니다.
예를 들어, 의미적으로 가깝다고 생각되는 고차원 공간에서의 두 샘플(A,B)간의 실제 Euclidean distance는 먼 경우가 많습니다.그 이유는 “curse of dimension”으로 인해 의미 있는 manifold를 찾지 못했기 때문이죠.
[추후에 Auto-Encoder 관련 글이 완성되면 manifold에 대한 보충 설명 글로써 링크를 걸어두도록 하겠습니다]

즉, 실제 Euclidean distance는 manifold 상에서 구해야 하기 때문에, manifold를 잘 찾는 것이 두 데이터간 유의미한 similarity를 구하는데 결정적인 역할을 할 수 있겠죠.

결국, 유의미한 manifold를 찾기 위해서는 dimension reduction 방식이 필요한데, 그것이 오늘날 자주 사용되는 deep neural network이죠.

결국, 특정 metric(ex: Euclidean distance)을 기준으로 한 유사도를 찾기 위해 deep learning model의 parameter들이 학습된다면, 이는 해당 meteric을 찾기 위한 manifold를 찾는 과정이라고 볼 수 있고, 이 과정 자체가 "estimated from the data"를 의미하기 때문에, learned metrics라고 볼 수 있는 것입니다.

다시 말해, deep metric learning이란 deep neural network를 이용하여 적절한 manifold를 찾아 metric learning을 연구하는 분야라고 정리할 수 있습니다.
UIUC 대학의 SVETLANA LAZEBNIK 교수의 similarity learning ppt자료를 살펴보면 deep neural network를 이용하여 metric learening을 하는 것을 확인해 볼 수 있습니다.

[deep metric learning의 예시]
먼저, 유사한 이미지를 한 쌍으로 한 positive pair 끼리는 Euclidian Loss가 최소화가 되도록 학습 시키면, deep neural network는 고차원 원본 데이터 positive pair끼리 거리가 가깝도록 low dimension으로 dimension reduction(or embedding) 할 것입니다. 즉, positive pair끼리는 Euclidian loss가 최소화 되게 parameter들이 학습된 것인데, 이것을 원본 데이터로 부터 추정(estimation)되었다고 볼 수 있기 때문에 learned metric이라고 한 것이죠.

또한, negative pair 끼리는 Euclidan distance 값이 커지도록 설정해줄 수 있습니다. 아래 수식을 보면, margin (m) 이라는 개념이 도입되는데, margin은 negative pair간의 최소한의 거리를 의미합니다. 예를 들어, 우리는 loss 값이 최소가 되기를 바라는데, negative pair (xn, xq) 의 거리가 m 보다 작다면 계속해서 loss 값을 생성해낼 것 입니다. 그런데, 만약 학습을 통해 negative pair 간의 거리가 m 보다 크게 되면 loss 값을 0으로 수렴시킬 수 있게되죠.
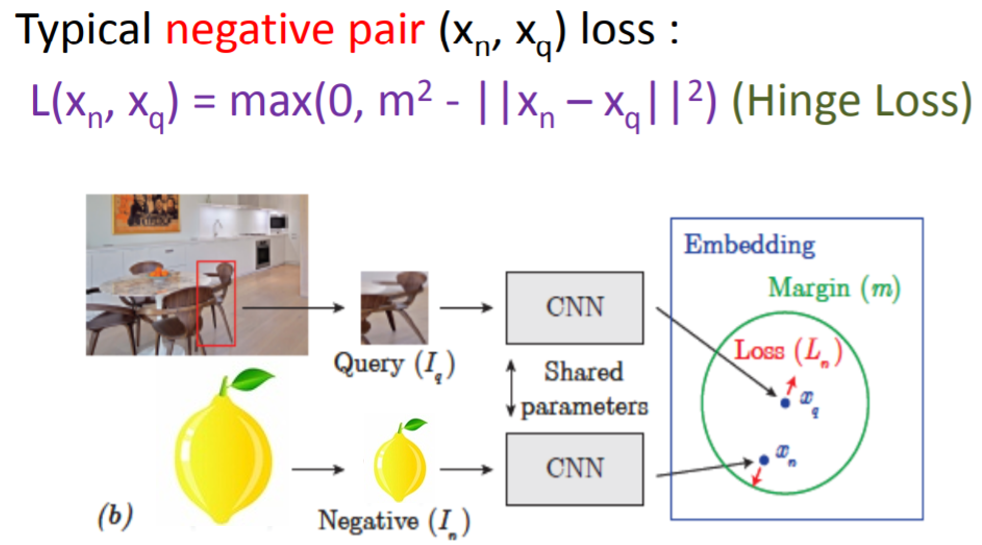
위에서 언급한 두 수식을 결합한 loss를 contrastive loss라고 합니다.

쉽게, contrastive loss를 통해 학습을 한다는 것은 두 데이터가 negative pair일 때, margin 이상의 거리를 갖게 하도록 학습하는 것과 동일하다고 할 수 있습니다.

Pytorch에서는 negative pair 뿐만 아니라, positive pair에 대한 margin 값도 설정해놓고 있습니다. (참고로 아래 LpDistance는 Euclidean distance를 의미합니다)

(↓↓↓ Pytorch metric learning loss ↓↓↓)
https://kevinmusgrave.github.io/pytorch-metric-learning/losses/#contrastiveloss
Losses - PyTorch Metric Learning
Losses All loss functions are used as follows: from pytorch_metric_learning import losses loss_func = losses.SomeLoss() loss = loss_func(embeddings, labels) # in your training for-loop Or if you are using a loss in conjunction with a miner: from pytorch_me
kevinmusgrave.github.io
참고로, margin이라는 개념을 이용하게 되면 경우에 따라 negative pairs의 관계를 크게 3가지로 나눌 수 있습니다.
- d: distance를 구하는 함수
- a: positive, negative pair의 기준이 되는 데이터
- Hard Negative Mining: positive pair에 해당하는 margin 안에 negative sample이 포함되어 있는 경우
- Semi-Hard Negative Mining: positive pair margin 범위 안에 속하진 않지만, negative pair margin 범위 안에도 속하지 않는 경우
- Easy Negative Mining: negative pair margin 범위에 속하는 경우

결국, contrastive loss를 이용하여 deep metric learning을 하게 되면 아래 그림 같이, 유사한 데이터들끼리 clustering이 될 것 입니다.
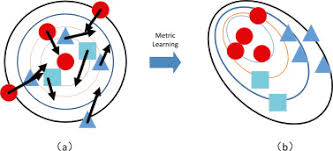
사실, contrastive loss라는 용어와 개념은 "Dimensionality Reduction by Learning an Invariant Mapping"이라는 논문에서 기원했습니다. 아래 논문의 저자로 우리가 익히 알고 있는 'Yann LeCun' 교수님도 있으시네요.
“Contrastive loss (Chopra et al. 2005) is one of the earliest training objectives used for deep metric learning in a contrastive fashion.”

앞서, 소개한 contrastive loss는 contrastive learning의 한 종류입니다.
즉, contrastive learning 이라는 것은 데이터들 간의 특정한 기준에 의해 유사도를 측정하는 방식인데, contrastive loss는 positive pair와 negative pair 간의 유사도를 Euclidean distance 또는 cosine similairty를 이용해 측정하여, positive pair 끼리는 가깝게, negative pair 끼리는 멀게 하도록 하는 deep metric learning (or learned metric) 이라고 정리할 수 있습니다.
(참고로, contrastive learning을 굳이 deep neural network로 하지 않아도 되지만, deep neural network의 강력한 효용성 때문에 deep neural network를 기반으로한 deep metric learning 방식인 contrastive learning을 하려고 하는 것이 죠.)
Positive pair 끼리는 가깝게, negative pair 끼리는 멀게 하도록 하는 deep metric learning (or learned metric) 기반의 contrastive learning 종류는 굉장히 다양합니다. 즉, 유사도를 측정하는 방식이 다양하죠. 예를 들어, infoNCE는 mutual information이라는 개념을 기반으로 유사도를 측정합니다. (Triplet loss는 이미 similarity learning에서 간단히 설명한 바 있습니다). (Mutual information 관련 설명은 다음 글에서 하도록 하겠습니다).

지금까지의 설명을 기반으로 봤을 때 deep metric learning 기반의 contrastive learning이라는 분야를 다룰 때 중요하게 다루어야 하는 개념이 두 가지가 있습니다.
- Similarity Measure (Metric)
- Contrastive learning은 positive pair 끼리는 가깝게, negative pair 끼리는 멀게 하도록 해주는 것이 목적입니다.
- 이 때, positive pair라는 것을 상징하는 유사도 값의 종류는 굉장히 다양합니다.
- ex1) Euclidean distance → Contrastive loss
- ex2) Mutual information → infoNCE
- Dimension Reduction (deep neural network; Nonlinear dimension reduction)
- Contrastive learning 즉, 데이터들 간의 유사도를 비교하는데 있어서 굳이 deep neural network를 사용할 필요는 없습니다.
- 하지만, 고차원 데이터들 간의 유사도를 비교하는 것은 쉬운일이 아닙니다.
- 그래서, 유사도 기준에 알맞도록 고차원 데이터를 저차원으로 dimension reduction 하는 방법이 중요합니다.
- Deep neural network는 이미지와 같은 고차원 데이터를 저차원 feature로 embedding 할 수 있는 강력한 dimension reduction 기능을 갖고 있습니다.
(↓↓↓ 딥러닝 외 nonlinear dimensionality reduction 방식 ↓↓↓)

개인적으로는, contrastive learning을 연구하기 위해서는 두 가지 key word 인, "Metric learning", "Deep Neural Network"에 초점을 맞추는게 중요하다고 생각합니다.
지금까지 Contrasitve learning에 대해 간단히 정리해봤습니다.
이번 contrastive learning에서는 유사도를 Euclidean distance를 기준으로 한 contrasitve loss를 소개했습니다.
다음 글에서는 contrastive learning 중에 mutual information을 유사도의 기준으로 삼은 다양한 loss에 대해 소개해 보도록하겠습니다.
감사합니다.
[Reference site]
Contrastive Representation Learning
The main idea of contrastive learning is to learn representations such that similar samples stay close to each other, while dissimilar ones are far apart. Contrastive learning can be applied to both supervised and unsupervised data and has been shown to ac
lilianweng.github.io
https://slazebni.cs.illinois.edu/spring17/lec09_similarity.pdf
'Self-Supervised Learning > Contrastive learning (2018~)' 카테고리의 다른 글
| 1. Mutual information (0) | 2021.10.04 |
|---|