Time Traveler

안녕하세요.

이번 장에서는 이산확률분포를 설명하기 위한 여러 개념들에 대해서 살펴보도록 하겠습니다.

1. 확률분포를 사용하는 이유

• 우리는 사회현상, 자연현상을 분석하기 위해 통계적 개념을 이용합니다.
• 예를 들어, 정규(확률)분포는 '일반적인 사회현상을 통계로 나타낼 때, 대부분 평균 주위에 가장 많이 몰려 있고, 그 수치가 평균보다 높거나 낮은 경우는 점점 줄어들게 되는 현상'을 나타내는데, 이러한 현상을 보여주는 확률 분포로써 '정규(확률)분포'를 사용합니다. (정규(확률)분포에 대해서는 연속확률분포를 다룰때 자세히 설명하도록 하겠습니다.)

• 통계학에서는 다양한 확률분포를 사용합니다. 당연히 다양한 자연현상과 사회현상이 있기 때문에, 이러한 현상들을 대표하는 확률분포도 다양하겠죠.
• 그럼 지금부터 확률분포에 대해서 천천히 알아보도록 하겠습니다.

2. 확률분포(Probability Distribution)

• 실험(시행)을 통해 확률변수(random variable) 값이 정해지면, 그 값들의 빈도수를 기반으로한 확률함수를 통해 각각의 변수에 대한 확률 값이 정해집니다.
• 아래 그림에서는 몸무게에 해당하는 정수 값들 (50,60,70,80)이 random variable이며, 상대도수 값이 확률 값입니다.

• 위의 설명을 좀 더 직관적으로 표현하면 아래와 같습니다.

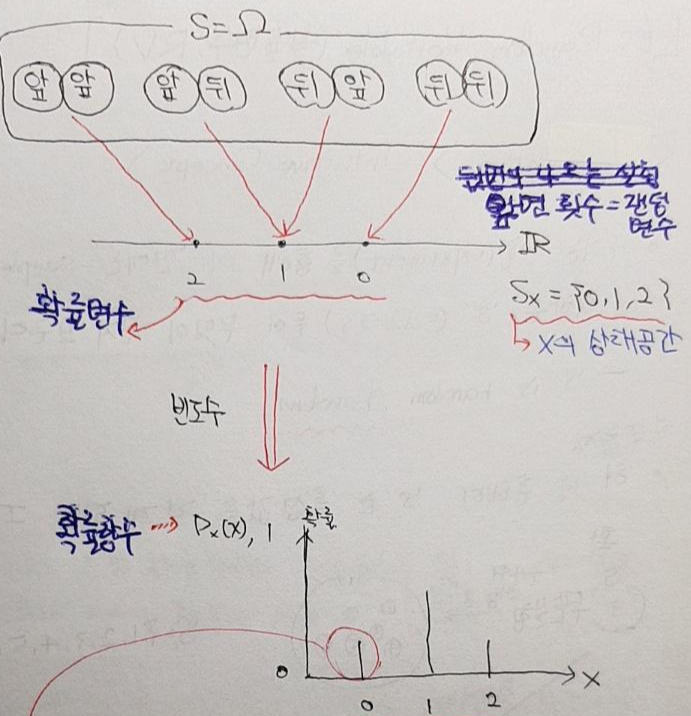
• 실험 데이터들이 많아지면 확률 변수에 따른 확률 값들의 분포를 짐작할 수 있게 됩니다.
• 이러한 실험을 통해서 얻은 확률분포 자체만으로도 굉장히 유용하게 쓰이지만, 해당 확률분포를의 expectation, variance 등의 개념들을 이용하여 유의미한 통계 작업을 하게 됩니다. (expectation, variance 에 대한 설명은 뒷 부분에서 하도록 하겠습니다)

3. Probability Mass Function (PMF)

• 이전 글("2. 확률분포")에서 확률 함수에 대해서 앞서 설명했기 때문에 확률함수에 대한 설명은 생략하도록 하겠습니다. PMF는 간단히 말해 확률 함수가 취하는 정의역이 이산확률변수(discrete probability variable)일 뿐입니다.
  • Probability Mass Function describes a probability distribution over discrete variables.
• 밀도라고 이름을 붙인 이유는 사실 연속확률분포와 관련된 PDF (Probability Density Function)를 먼저 살펴봐야 하는데, 먼저 여기에서는 간단히 "정의" 정도만 언급하고 자세한 설명은 연속확률분포 파트에서 설명하도록 하겠습니다.
• 연속확률분포에서 사용되는 PDF는 밀도라는 개념을 이용합니다. '밀도'라는 것은 부피당 차지하는 질량의 정도(=질량/부피)를 말합니다. 연속확률분포에서는 면적이 확률 값이 되는데 아래 그림을 보면 면적에 해당하는 공간(부피)에 무수한 선들이 빽빽하게 채워져있는 것 처럼 보이게 됩니다. 

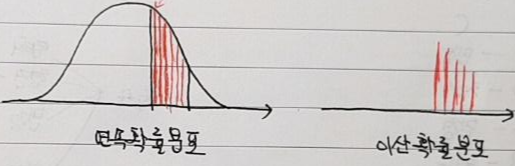
• 이산확률분포에서는 질량에 해당하는 하나의 선 자체가 확률 값이 되기 때문에 해당 질량(확률 값)을 도출하는 확률 함수를 PMF라고 부르게 됩니다. 
• PMF는 어떤 discrete random variable에 대한 probability model이라고 할 수 있습니다.

4. 이산확률분포(Discrete Probability Distribution) with PMF axiom

• 우리는 실험을 통해서 확률변수(random variable)을 얻게 됩니다.
• 보통 확률변수를 변량(variance)라고도 하는데, 예를 들어, 몸무게를 측정하는 실험을 통해 얻은 변량 or 확률변수는 50, 60, 70, 80이 될 수 있습니다.
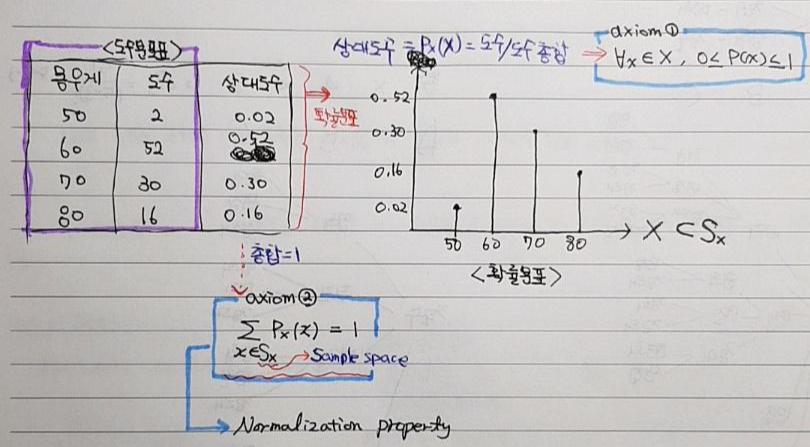
• 만약, 우리가 100명에 대해서 조사한다고 했을 때, "몸무게 50에 해당하는 사람이 2명, 60에 해당하는 사람이 52명, 70에 해당하는 사람이 30명, 80에 해당하는 사람이 16명"이라고 했을 때, 해당 확률변수(50,60,70,80)의 사람 수는 일종의 (빈)도수(frequency)가 됩니다.
• 이러한 확률변수에 대한 (빈)도수를 표로 정리한 것이 도수분포표입니다.
• 그리고 이러한 도수분포표는 상대도수(=도수/도수총합)를 통해 확률 값으로 변경되는데, 이 때 상대도수를 도출하기 위한 함수를 확률함수(PMF)로 볼 수 있습니다.
• 그리고 이러한 PMF에는 아래 그림에서와 같이 두 가지 공리(axiom①, axiom②)가 존재합니다. 그러므로 다음글에서 소개할 다양한 이산확률분포의 확률함수는 아래 두 가지 공리가 항상 성립해야합니다.
  • 특히, 도수에서 상대도수로 바꿀 때, 각각의 도수를 도수총합(=N)으로 나누는데 이를 normalization(정규화)이라고 합니다.

• 앞서 "실험을 통해 얻은 확률분포에서 expectation, variance 등의 개념들이 출현하게 되는데, 이러한 개념들을 이용하여 유의미한 통계 작업을 하게 됩니다."라고 언급했는데, expectation과 variance가 어떻게 쓰이는지 알아보기 전에, expectation과 variance가 무엇인지 먼저 알아보도록 하겠습니다.

5. Expectation (기댓값)

• 기댓값 E(X)를 보통 평균(mean)이라고 합니다.
• 만약 한 반의 시험점수 '평균'이 70점이라고 한다면, 해당 반의 학생 중 아무나 한명을 골랐을 때 시험점수가 70점일거라고 '기대'하기 때문에, '평균'과 '기대값'이라는 용어를 동일시합니다.

5-1. Linearity of expectations

• 선현성에 대한 개념은 나중에 선형대수라는 과목을 다룰 때 더 자세히 설명하도록 하고, 여기에서는 기댓값과 관련된 성질을 알아보는 차원정도로 정리해보도록 하겠습니다.

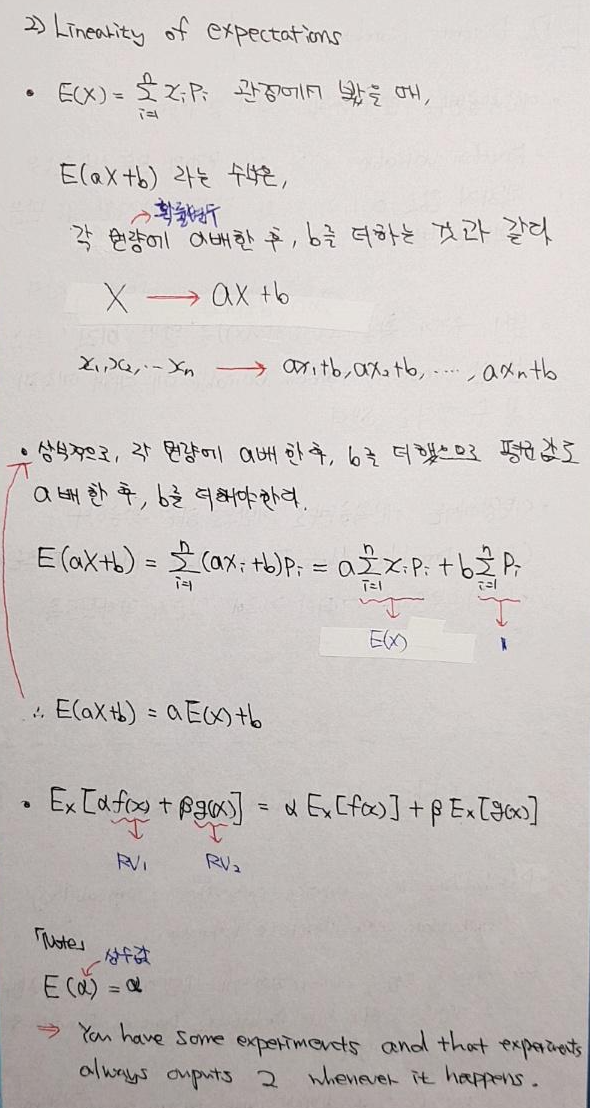
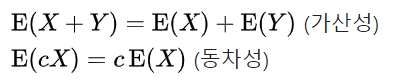
• 평균(기댓값)이 통계적으로 의미가 있는 이유는 데이터들의 분포를 대표할 수 도 있기 때문입니다.
• 예를 들어 아래 그림에서는 평균이 (대략) 175정도 된다고 볼 수 있는데, 아래와 같은 정규(확률)분포표를 따른다고 하면 실험을 통해 수집한 데이터들이 175에 몰려있다는 것을 추론할 수 있게 됩니다.
• 즉, 평균(기댓값)이 데이터들의 분포를 대표할 수 있게 됩니다. 

6. 편차(Deviation)와 분산 (Variance)

• 앞서 살펴본 '키'관련 확률분포표에서 평균(기댓값)은 데이터들의 분포를 대표할 수 있다고 설명했습니다.
• 아래와 같은 상황에서 A확률 분포는 평균(기댓값)이 데이터들의 분포를 대표할 수 있다고 말할 수 있겠는데, B확률분포를 상대적으로 봤을 때 평균(기댓값)이 데이터의 분포를 대표한다고까지 할 수 있을지 잘 모르겠습니다. 

• B확률 분포와 같은 경우는 평균과 데이터들의 거리가 매우 멀기 때문에, 평균값이 데이터들의 분포를 대표한다고 자신있게 말하기 어렵습니다.
• 그래서 B와 같은 확률 분포를 대표하기 위해서 '평균'과 '평균으로부터 떨어져 있는 데이터들의 거리정도'를 사용해야 B 확률분포를 상징(represent)할 수 있게 됩니다.
• 이때 '평균과 데이터들의 거리'를 '편차'라고 하는데, 해당 확률분포가 평균과의 '편차'가 얼마나 심한지 알기 위해서는 '편차'의 평균을 구하면 됩니다.
• 그런데 아래 그림에서보면 알 수 있듯이 편차가 분명 존재함에도 불구하고 편차들의 평균값이 0이 나올 수 있습니다. (아래 그림에서 변량(확률변수=random variable)은 몸무게에 해당하고, 몸무게의 평균은 70입니다)
• 사실 아래 예시 뿐만아니라 모든 경우에도 편차(변량-평균)의 평균값은 '0'이라는 걸 알 수 있습니다.

• 결국, 편차의 대푯값을 구하기 위해 편차에 존재하는 음수를 양수로 바꾸자는 idea가 나오게 되었고, 음수를 제곱하여 편차의 대푯값을 구하는 '분산'이라는 개념이 나오게 되었습니다. 
• 모든 편차에 제곱을 해주면 항상 양수가 나오기 때문에 아래와 같이 계산하는 방식을 분산이라고 정의하게 됩니다.

• 분산(variance) 공식은 아래와 같이 정리할 수 있습니다.

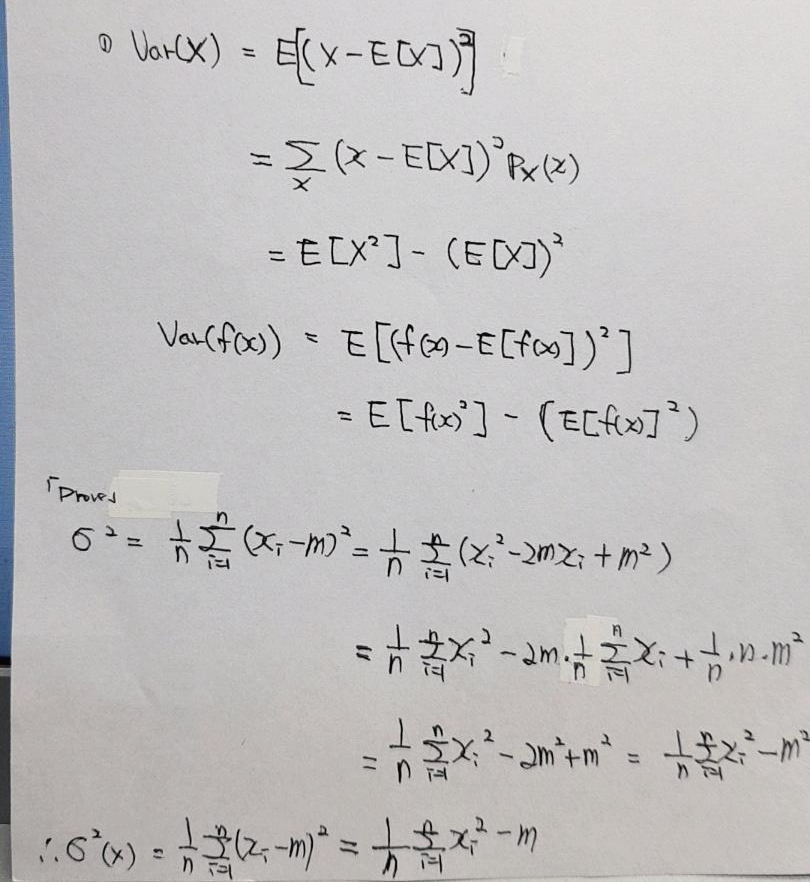
• 분산은 아래와 같은 속성을 지닙니다.

• 통계학에서는 평균(기댓값)과 분산을 통해 유의미한 연구를 진행하게 됩니다.

7. 표준편차 (Standard deviation)

• 분산식을 보면 제곱 성질로 인해 값이 커진다는 것을 알 수 있습니다.
• 그렇기 때문에 분산식에 루트 (√) 를 씌워주어 값의 크기를 줄여주는데, 이것을 표준편차라고 합니다.
• 즉, 평균으로부터 데이터들이 얼마나 떨어져 있는지의 정도를 표준적으로 알려준다는 의미를 지닙니다.
• 표준편차를 구할 때 식을 RMS (Root Mean Square)이라고도 부릅니다.

이번 장에서는 이산확률분포에 대한 개념과, 확률분포에서 사용되는 유의미한 개념들(평균, 분산, 표준편차)에 대해서 알아보았습니다. 그럼 다음 글에서부터는 이산확률분포의 여러 종류들에 대해서 알아보도록 하겠습니다.

안녕하세요.

이번 장에서는 확률분포에 대한 개념을 설명보겠습니다.

확률분포에 대한 개념을 설명하기에 앞서, 확률변수에 대해서 설명을 해보도록 하겠습니다.

1. Random Variable

• Ways of assigning numerical results to the outcomes of an experiment = A function from the sample space (Ω) to the real numbers (R).
  • 우리가 사람에 대해서 어떠한(임의의(random)) 실험을 한다고 해보겠습니다.
  • 사람의 키를 측정하는 실험을 할 수 도 있고, 몸무게를 측정하는 실험을 할 수 도 있습니다.
  • 즉, 사람이라는 변수 는 어떤 실험을 하는지에 따라 굉장히 다양한 값 (randomness)을 가질 수 있습니다.
  • 만약, '키 측정 실험'을 하게 되면 특정 실수 값 (키) 을 갖게 됩니다. 예를 들어, 우리가 실험을 통해서 얻은 결과가 "키={150~190}"의 범위를 갖을 수도 있습니다. 
• [요약1] 결국, 임의의(random) 실험에 따라서 다양한 변수(variable: 몸무게 or 키 or etc..) 들을 갖게되기 때문에 키, 몸무게와 같은 것들을 하나의 random variable이라고 부릅니다.
• [요약2] 키와 몸무게라는 random variable 종류에 따라 실수 값(or 범위: 키={150~190}, 몸무게={40~80)) 이 정해지기(mapping되기) 때문에 해당 random variable을 하나의 함수라고 보기도 합니다.

2. Probability Variable

• 앞서 Random variable은 '몸무게', '키'와 같은 하나의 함수라고 했습니다.
• Probability variable은 위와 같은 함수(random variable)을 통해 얻은 실수 값이라고 할 수 있습니다.
• 그런데, 어떻게 실수 값 자체가 또다른 변수(probability variable)가 될 수 있을까요?
• 해당 실수 값에 해당 하는 경우가 얼마나 빈번하게 일어나는지 확률함수(\(P{_X}(X=x)\))을 통해 알아 낼 수 있기 때문에, '실수 값' 자체도 확률 값을 알아내기 위한 변수(variable)가 될 수 있습니다.

• 결국, random variable 함수 = 실수 값 = probability variable 이기 때문에, random variable과 probability variable을 따로 구별하지 않고 동의어로 사용하기도 합니다.

3. 확률변수(Random Variable)의 종류

• 확률변수는 크게 두 가지 종류로 나뉩니다.
• 이번 글에서는 각각의 확률변수에 대한 정의만 설명하고, 다음 글에서 이산확률분포를 설명하면서 더 자세히 다루도록 하겠습니다.

3-1. 이산확률변수 (Discrete Random Variable)

• Random variable X가 어느 특정 구간의 모든 실수 값을 택하지 않고 0, 1, 2, ..  와 같은 이산적인 값만을 택하는 변수입니다.

3-2. 연속확률변수 (Continuous Random Variable)

• Random variable X가 어느 특정 구간의 모든 실수 값을 취하는 연속된 구간의 값을 취하는 변수입니다.

4. 확률분포 (Probability Distribution)

• Probability distribution이란 확률변수(random variable)의 모든 값과 그에 대응하는 확률들이 어떻게 분포하고 있는지를 말합니다.
• 앞서 정의한 확률변수의 종류에 따라 확률분포의 종류도 크게 두 가지 (이산확률분포, 연속확률분포)로 나뉘어 집니다.

다음 글에서 부터는 본격적으로 이산확률분포에 대한 개념과, 다양한 이산확률분포를 다루면서, 어떠한 상황속에서 해당 확률분포들을 사용하는지 알아보도록 하겠습니다!

안녕하세요~

이번 장에서는 확률의 개념과 관련된 전반적인 용어 설명들을 하도록 하겠습니다.

1. 확률의 기원

확률이라는 학문은 도박을 그 기원으로 두고 있는데요. 이에 대한 설명이 담긴 영상을 보도록 하겠습니다.

https://www.youtube.com/watch?v=F8TMnn8SW4c 

2. 확률의 사전적 의미

• 확률의 한자 뜻은 다음과 같습니다.
  • 확실할 "확" + 비율 "율" = 확실함의 비율(정도)
• 다음은 영어에서 정의하는 확률의 뜻을 살펴보도록 하겠습니다.
  • Probability is the measure of the likelihood(=%) that an event in sample space will occur.
• 여러 해석이 가능하겠지만 위의 두 설명을 한 단어로 설명하자면 '가능성의 정도'라고 할 수 있겠네요. 당연히 수학분야에서 사용되기 때문에 '정도'를 수치로 표현할 것이구요.
• 가능성이라는 것이 갖는 특징은 어떤 행위가 비결정적인 결과를 낳을 때 사용 가능한 용어라는 점입니다. 
  • 비결정적 결과: 주사위를 던지는 행위
  • 결정적 결과: 물리법칙 → \(E=mc^2 \)

3. 수학적 확률(가능성) = 라플라스 확률

• 위에서 정의한 사전적 정의를 좀 더 구체적으로 표현하면 아래와 같습니다.
  • 확률실험(시행: trial)을 통해 얻은 모든 실험결과(표본공간: Sample space)들 중에서 특정사건(event)이 일어나는 것에 대한 확신(믿음)의 정도(가능성: probability)를 의미 → 어떤 사건(event)이 일어날 가능성을 수치로 나타낸 것
    • 용어1. 확률실험 (시행: trial): 우연의 요소(비결정적 결과→아래에서 설명)를 포함하는 실험으로써 아래 두 가지를 만족하는 실험
      • 1. 같은 조건에서 반복시행이 가능한 실험
      • 2. 매 실행 결과가 무엇이 될지는 알 수 없으나, 실현 가능한 모든 결과들을 시행전에 알 수 있는 실험
      • 3. ex) 주사위 확률시험
    • 용어2. Sample space=표본공간 (Ω,s)
      • Sample space는 확률실험(trial)에서 실현 가능한 모든 결과를 원소(element)로 갖는 집합(set)이다.
      • ex) 주사위 던지는 실험에서의 표본 공간 Ω = {1,2,3,4,5,6}
    • 용어3. Event (사건) = 어떤 시행의 특정한 결과 (표본 공간의 부분집합을 의미)
      • ex) 주사위를 두 번 던졌을 때, "2,4"가 나왔다면 → E = {2,4}

• 위와 같은 정의하에 A사건이 나타날 확률을 표현하는 수학적 확률의 정의는 아래와 같습니다.
  • A의 수학적 확률 = P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{사건 A의 원소 개수}{표본공간의 원소 개수}\) = \(\frac{사건 A가 나타나는 경우의 수}{전체의 경우의 수}\)

• 고등학교때 확률을 배우기 전에 경우의 수를 왜 배우는지 아시겠죠?  아래 목록들은 중고등학교 교과과정에서 배우는 경우의 수 인데,여기에서는 몇몇 부분만 뒷 부분에서 다루도록 하겠습니다.
  • 합의법칙과 곱의법칙
  • 순열, 원순열, 같은 것을 포함하는 순열, 최단 경로의 수, 중복순열
  • 조합, 도형의 개수, 중복조합
  • 분할, 색칠문제, 좌석배치, 숫자 만들기, 이항정리, 이항계수의 성질

4. 확률의 기본 두 가지 이론 

• 확률의 근간을 이루는 이론 중에 가장 기본이 되는 두 가지 확률이론 있습니다.
  • 두 사건의 합집합 (A라는 사건이 일어나거나, B사건이 일어날 경우) 에 대한 확률→ 확률의 덧셈정리
  • 두 사건의 교집합 (A, B 사건이 동시에 일어날 경우 OR A 사건이 일어나고, 연속해서 B 사건이 일어날 경우) 에 대한 확률 → 확률의 곱셈정리  
• 지금부터 이 두 가지 이론에 대해서 알아보도록 하겠습니다.

4-1. 덧셈정리(Addition theorem of probability) with 배반사건(Exclusive evnet)

• A라는 사건이 일어나거나(OR) B라는 사건이 일어날 경우의 확률을 구할 때
• \(\frac{n(A\cup B)}{n(S)}\) = \(\frac{n(A)}{n(S)}\) + \(\frac{n(B)}{n(S)}\) - \(\frac{n(A\cap B)}{n(S)}\)
• \(P(A\cup B) = P(A) + P(B) - P(A\cap B)\)
• 덧셈정리과 관련해서 알아두어야 할 한 가지 개념이 있습니다.
  • 배반사건(Exclusive Event)
    • 우리가 A라는 사건이 일어나거나 B라는 사건이 일어날 확률을 구한다고 했을 때, A라는 사건과 B라는 사건이 동시에 일어나지 않을 수도 있습니다. 이름 그대로 두 사건이 접점이 없이 서로 배타적임을 의미합니다.  그리고, 이러한 개념을 수학적으로 표현하면 다음과 같습니다. → \(P(A\cap B) = 0\)
    • ex) 주사위를 던졌을 때 홀수가 나오거나 (=A사건), 짝수가 나올(=B사건) 경우 A, B 사건을 배반 사건이라 할 수 있습니다.
    • 그래서 A와 B가 서로 배반사건인 상황에서의 덧셈정리는 다음과 같이 정리할 수 있습니다.
      • \(P(A\cup B) = P(A) + P(B)\)  

4-2. 곱셈정리(Multiply theorem of probability) with 종속사건(Dependent event), 독립사건(Independent event), 조건부확률(Conditional probability)

• 확률엥서 곱셈을 하는 경우는 A와 B사건이 동시에 일어날 경우입니다. 
• 또한, 확률 곱셈은 A라는 사건이 일어나고 연속적(순차적)으로 B라는 사건이 일어날 확률을 구할 때도 사용합니다.
• 예를 들어, 아래 그림과 같이 서울에서 대전으로 갈 때 1, 2, 3 맛집이 있고, 대전에서 부산으로 갈때 4, 5라는 맛집이 있다고 하겠습니다. 아침은 A 맛집에서 먹고 점심은 D 맛집에서 먹을 수 있는 확률은 어떻게 될까요?

• 확률의 곱셈정리와 관련해서 알아야할 개념이 있습니다.
  • 위에서 설명한 곱셈정리는 독립사건을 가정하고 있습니다. 그렇다면 독립사건은 무엇일까요?
  • 독립사건을 알아보기 전에 종속사건을 먼저 살펴보겠습니다, 종속사건을 설명하려면 조건부 확률을 알고 있어야 하니 "조건부확률 → 종속사건 → 독립사건" 순서로 글을 정리해보도록 하겠습니다.

4-2-1. 곱셈정리(Multiply theorem of probability) with 종속사건(Dependent event), 독립사건(Independent event), 조건부확률(Conditional probability)

• 확률 곱셈을 이용하여 독립사건, 종속사건, 조건부확률을 알아보도록 하겠습니다 
  
  • 용어1. 조건부확률: B라는 사건이 주어졌을 때 A사건이 일어날 확률
    • Probability of A, Given that B occured
    • P(B|A)
    • 아래 영상에서 조건부 확률과 관련된 재미난 영상을 한 번 확인해보셔도 좋을 것 같습니다.

https://www.youtube.com/watch?v=5DSYQx0iL7I

• • 용어2. 종속사건: A라는 사건이 B라는 사건에 영향을 줄 때 → 즉, 두 사건이 일어나는 순서에 따라 서로 영향을 주고 받을 때, A와 B는 종속사건이라고 합니다.
    • 예를 들어, 52장의 카드를 첫 번째 뽑은 (A사건) 결과가, 두 번째 뽑을 경우의 (B사건) 에 영향을 미치는 경우 → ex) A사건의 표본공간 = 52, B사건의 표본공간 = 51
     Q. 52장의 카드를 순차적으로 뽑는다고 했을 때 모두 검은색이 뽑힐 확률은?

• 용어3. 독립사건: A라는 사건이 B라는 사건에 영향을 주지 않을 때 → 즉 두 사건이 서로 관계가 없이 독립적일 때  
  • 예를 들어, 첫 번째 주사위를 던졌을 때 앞면이 나왔다고 했을 때 (A사건), 두 번째 주사위를 던졌을 때 앞면이 나올 결과에 (B사건) 어떠한 영향도 미치지 않음

5. 독립시행 확률 (베르누이 확률, Binomial Probability) with 순열(Permutation), 조합(Combination)

• 앞서 독립사건에 대해서 알아보았습니다.
• 그렇다면, 독립사건인 상황(조건)에서 사용할 수 있는 확률 개념인 '독립시행 확률'에 대해서 알아보도록 하겠습니다. 
• 우선, 독립시행 확률을 이해하기 위해 순열, 조합에 대한 개념부터 알아보겠습니다.

5-1. 순열

• 순서를 고려하여 나열한 경우의 수 (= 줄 세우는 방법의 수 = 자리 바꿈하는 방법의 수)
  • n명에서 r명을 뽑아 줄 세우는 방법의 수 = \(_{n}P_{r}\) = \(\frac{n!}{(n-r)!}\)
  • ex) "철수, 영희, 민정, 현진, 정태"가 A, B, C 에 앉을 수 있는 경우의 수는?순열

5-2. 조합 (Combination)

• 순서에 상관없이 구성원을 뽑기만 하는 경우
• n명에서 r명을 뽑는 경우의 수 = \(_{n}C_{r}\) = \(\frac{n!}{(n-r)!r!}\) = \(_{n}C_{n-r}\)
• 순열을 또 다른 관점에서 보면 크게 두 가지 action으로 분류할 수 있습니다
  • \(_{5}P_{3}\) → 5명 중 3명을 선택하는 경우의 수 × 뽑힌 3명을 일렬로 나열 하는 수 = \(_{5}C_{3}\)×3!
  • 이러한 관점으로부터 조합 공식을 유도할 수 도 있음

5-3. 독립시행 확률(베르누이 확률, Binomial probability)

• 우리 인생에서 알고 싶은 확률들이 보통은 성공 또는 실패할 확률입니다.
• 이러한 조건에서 공(나온)에 대한 확률이 고정되어 있다고 가정해보겠습니다. 
• 이때 고정된 성공 또는 실패의 확률을 갖고 있는 독립인 사건을 여러 번 시행했을 때 얻은 확률을 독립시행 확률이라 합니다.
• \(_{시행횟수}C_{성공횟수}\)×\(성공확률^{성공횟수}\)×\(실패확률^{실패횟수}\)
• 시행횟수=n, 성공횟수=r, 실패횟수=k, 성공확률=p, 실패확률=p-1 이라고 했을 때
• \(_{n}C_{r}\)×\(p^{r}\)×\((p-1)^{k}\)

6. 전체 확률의 법칙 = 전확률 정리 (Law of Total Probability)

• 전확률 정리는 조건부 확률 (Conditional probability) 로부터 조건이 붙지 않는 확률 (Unconditional probability) 을 계산 할 때 쓸 수 있습니다.
• When we face a complicated problem, sometimes, it gives us simple solution that the complicated problem is broken up simpler pieces. → 베이즈 정리에서 전확률 정리를 이용함 (바로 뒷 부분에서 베이즈 정리 설명)

7. 베이즈 정리

• 우리가 현재 어떤 사건 A에 대학 사전 확률(prior knowledge)을 알고 있다고 하겠습니다.
• 사전 확률은 말그대로 지금까지의 경험을 바탕으로 설정된 A사건에 대한 확률 값입니다.
• 즉, 앞으로의 경험(데이터)에 따라 A사건에 대한 확률 값은 변경(updating)될 수 있습니다.
• 즉, 우리는 이전에 갖고 있었던 사건A에 대한 우리의 믿음의 정도 (사전확률)를 새로 경험하여 얻는 정보(data)에 따라 updating을 해야, 사건A에 대한 확률 값이 점점 신뢰성을 갖게 될 것입니다.
• 정리하자면, 새로운 정보를 얻었을 때 베이즈 정리를 이용해 해당 사건에 대한 최신 확률 값을 얻을 수 있습니다.
• 예시
  • H라는 사건이 일어날 확률 = P(H) 
  • H라는 사건이 참이라는 조건하에 D가 일어날 수 있는 확률 = P(D|H)
  • D라는 데이터가 주어졌을 때 H가 일어날 확률 = P(H|D) = \(\frac{P(H\cap D)}{P(D)}\) = \(\frac{P(H)P(D|H)}{P(D)}\)
  • 분모가 되는 P(D) 부분을 전확률 정리로 풀어 쓸 수 있다 → 자세한 것은 문제를 통해 설명

8. 통계적 확률

• 주사위를 한 번 던졌을 때 1이 나올 확률이 6이라고 알고 있습니다. 다시말해, 주사위를 6번 던져야 1이 한 번 나올 것이라는 말과 같다고 할 수 있습니다.
• 하지만 현실에서는 주사위를 6번 던져도 1이 나올 확률이 1/6이 안될 수 도 있습니다.
• 여기에서는 주사위를 6번 던졌으니 시행횟수가 6입니다. 그런데, 이 시행횟수를 한 없이 늘리다보면 결국 1이 나올 확률이 우리가 알고 있는 수학적 확률인 1/6에 근사하게 됩니다.
• 즉, 어떤 시행(trial)을 여러 번 반복했을 때 \(\frac{나온횟수}{시행횟수}\) 는 시행횟수가 한 없이 커짐에 따라 특정한 값에 가까워지는데, 이를 통계적 확률이라 합니다. ex) 타율
• 실제로는 시행 횟수를 한 없이 커지게 할 수 없으므로 시행횟수가 충분히 클 때의 값을 통계적 확률로 봅니다.
• 결과적으로, 시행횟수가 커지다보면 결국 통계적 확률이 수학적 확률에 가까워진다는 철학이 깔려있습니다.

지금까지 확률에 대한 개념과 관련된 전반적인 개념을 다루었습니다. 다음 장에서는 확률분포라는 개념을 이해해보도록 하겠습니다.

[정리]

1. 확률은 "확률실험(시행: trial)을 통해 얻은 모든 실험결과(표본공간: Sample space)들 중에서 특정사건(event)이 일어나는 것에 대한 확신(믿음)의 정도(가능성: probability)를 의미" → 어떤 사건(event)이 일어날 가능성을 수치로 나타낸 것

• A의 수학적 확률 = P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{사건 A의 원소 개수}{표본공간의 원소 개수}\) = \(\frac{사건 A가 나타나는 경우의 수}{전체의 경우의 수}\)

2. 확률에는 두 가지 기초연산이 있다.

2-1. 덧셈정리(Addition theorem of probability) with 배반사건(Exclusive event)

• 확률에서 덧셈이 사용되는 경우: A라는 사건이 일어나거나(OR) B라는 사건이 일어날 경우의 확률을 구할 때
• \(\frac{n(A\cup B)}{n(S)}\) = \(\frac{n(A)}{n(S)}\) + \(\frac{n(B)}{n(S)}\) - \(\frac{n(A\cap B)}{n(S)}\)
• \(P(A\cup B) = P(A) + P(B) - P(A\cap B)\)
• 배반사건(Exclusive Event) = \(P(A\cap B) = 0\)

2-2. 곱셈정리((Multiply theorem of probability) with 종속사건(Dependent event), 독립사건(Independent event), 조건부확률(Conditional probability))

• 확률에서 곱셈이 적용되는 경우: A라는 사건이 일어나고 연속적(순차적)으로 B라는 사건이 일어날 확률을 구할 때 사용한다.
• 어떤 사건이 연속적으로 일어날 때 이전 사건이 다음 사건에 영향을 미치는 경우에 필요한 개념 및 수식
  • 종속사건(Dependent event) 
  • \(P(A\cap B)\) = P(B|A)P(A) = P(A|B)P(B)
  • 조건부 확률 (Conditional Probability): P(B|A) -> A라는 사건이 발생했을 때 B라는 사건이 발생할 확률
• 어떤 사건이 연속적으로 일어날 때 이전 사건이 다음 사건에 영향을 미치지 않는 경우에 필요한 개념 및 수식
  • \(P(A\cap B)\) = P(A)P(B)
  • 독립사건(Independent event) → P(B|A) = P(B)

3. 독립시행 확률 (베르누이 확률, Binomial probability)

• 고정된 성공 또는 실패의 확률을 갖고 있는 독립인 사건을 여러 번 시행했을 때 얻은 확률을 독립시행 확률이라 한다.
• 시행횟수=n, 성공횟수=r, 실패횟수=k, 성공확률=p, 실패확률=p-1 이라고 했을 때
• \(_{n}C_{r}\)×\(p^{r}\)×\((p-1)^{k}\)

4. 베이즈 정리 with 전확률 정리

• 이전에 갖고 있었던 사건A에 대한 우리의 믿음의 정도 (사전확률)를 새로 경험하여 얻는 정보(data)에 따라 updating할 수 있다.
• 즉, 새로운 정보를 통해 얻은 한 사건A에 대한 최신 확률 값을 베이즈 정리를 통해 얻을 수 있다.
• D라는 데이터가 주어졌을 때 H가 일어날 확률 = P(H|D) = \(\frac{P(H\cap D)}{P(D)}\) = \(\frac{P(H)P(D|H)}{P(D)}\)

안녕하세요.

이번에 확률과 통계에 대해서 글을 작성하려고 합니다.

제가 확률,통계를 블로그로 정리해야 겠다고 생각한 이유는 아래와 같이 몇 가지로 정리할 수 있을 것 같아요.

1. "AI, 데이터 사이언스, 머신러닝, 딥러닝"의 뿌리이기 때문

보통 AI, 데이터 사이언스, 머신러닝, 딥러닝을 응용수학이라고들 하는데

아마 여러 수학적 지식들이 복합적으로 적용되서 그런게 아닐까 싶어요.

예를 들어, 딥러닝의 어떤 모델 한 가지만 하더라도 선형대수, 통계학, 미적분학, 최적화 등등 정말 다양한 수학적 측면에서 해석할 수 있다는 뜻이죠.

2. 인간의 (철학적) 주장을 과학적으로 포장하기 위한 유일한 도구이기 때문

만약 제가 "비트코인이 주식보다 좋아?"라고 말했다고 해볼게요.

A라는 사람은 "비트코인이 더 좋아. 왜냐하면 비트코인은 수익성이 최대 130%까지 가능하거든"

이 말을 듣고 B라는 사람에게 비트코인을 하자고 했더니

B라는 사람이 "무슨소리야. 주식이 더 좋아. 주식 수익성이 최대 20%까지 이긴 해도 비트코인 처럼 단 시간에 원금 다 날리는 경우는 없거든"

이렇게 말했다고 해볼게요.

누구의 말을 믿어야 할까요? 

사실 누구의 말을 믿든 결국 자신의 철학에 따라 선택할 수 밖에 없을거에요.

만약 안정성에 더 우선순위를 두어야 하는 상황이라면 주식을,

주식의 최대 수익성이 아무의미 없는 경우는 비트코인에 투자하는게 더 좋을 거에요.

(빨간색: 주식/ 파란색: 비트코인 -> 100 원금 투자했을 때 우측으로는 이익, 좌측으로는 손실)

(아직 통계의 개념이 명확하지 않으신 분은 아래 그림을 굳이 이해하지 않으셔도 됩니다. 차차 설명해드릴게요!)

좀 더 설명해보자면...

보통 과거에는 많은 사람들이 안정성에 가치를 많이 두었기 때문에 주식을 많이 선택했을거에요. 

아무도 모르는 사람들이 주식을 해도 최소 -35%~25% 사이의 수익성이 보장됐기 때문에 원금을 날릴 경우가 없었기 때문이에요.

그런데 내가 아무리 25%의 수익성을 낸다고 해도 집값을 사는데 50년이 걸린다고 하면 이게 의미가 있을까요?

이러한 경우에는 손실을 감안하고 비트코인에 올인하려고 하는경우가 있을거에요. 

정치든, 과학이든, 마케팅이든 항상 자신의 아이디어(또는 주장)가 더 좋다는 것을 증명하거나

실제 사례를 보다보면 자신의 아이디어가 좋을 때도 있고 아닐 때도 있어요.

(또는 자신이 주장하는 인과관계가 타당하다고 인정을 받아야하는 경우도 있는데, 이러한 인과관계가 항상 성립하는 경우는 드물겠죠)

예를 들어, 화이자 백신이 좋다고는 하지만 어떤 사람들은 접종하면 사망하는 경우도 있습니다. 그렇다면 화이자 백신이 좋다고 할 수 있을까요?

여기서부터 화이자 사장은 통계 개념을 통해 다음과 같은 주장을 합니다.

"화이자를 맞았을 때 평균적으로 코로나에 걸릴 확률이 적습니다. 또한 다른 회사의 백신과 비교했을 때 코로나에 걸릴 확률이 적습니다. 그러므로 화이자 백신은 다른 백신들보다 더 좋다고 할 수 있습니다" 

결국 통계학이라는 도구를 통해서 무언가가 더 좋다 나쁘다고 하는 것은 절대적인 사실이 아니라

상대적인 관점에서 비교분석하여 얻어낸 결과라고 할 수 있습니다.

3. 확률을 품은 통계

결국 통계라는건 어떤 현상을 설명하기 위해 확률을 받아들인 학문이라고 보면 될 것 같아요.

그래서 제 개인적으로 통계학이라는 학문을 아래와 같이 받아들이고 있습니다.

"통계학은 인류를 위한 진실(확실성:certainty)을 만들기 위해 불확실성(uncertainty; 확률)과 타협한 학문"

다시말해 통계학은 확률(불확실성)을 기반으로 하여 어떠한 현상(집단)을 설명(대표)하기 위한 도구이며,

해당 현상(집단)들을 서로 비교 분석하여 자신들의 주장이 합리적임을 증명하기 위해 사용하는 도구라고 이해하고 있어요!

4. 국가를 통치하기 위해 만들어진 학문이 곳 통계학

https://www.youtube.com/watch?v=YlGMHmzeW3Y 

간단하게 이 글을 쓰기로한 동기에 대해서 작성해보았습니다.

그럼 본격적으로 다음 글에서 확률부터 천천히 글을 작성해 보도록 하겠습니다~