[통계학]3.정규분포를 따른다는 의미 (Feat. 중심극한정리)

안녕하세요.

이번 글에서는 정규분포에 대해서 설명하도록 하겠습니다.

본래 정규분포는 연속확률분포이기 때문에 확률편에서 설명하는 것이 맞지만, 통계편에서 설명드리는 이유는 아래와 같습니다.

• 정규분포는 연속확률분포입니다.
• 하지만, 정규분포를 사용한다는 것에는 다양한 통계적 철학(사고)를 전제하고 있습니다.
• 그렇기 때문에, 통계학 파트에서 다루는 것이 좋다고 판단했습니다.

이미지 출처: https://regressiontoyou.tistory.com/30

 

그럼 지금부터, 정규분포에 대한 수학적 정의를 설명하기 앞서, 왜 정규분포가 통계에서 사용되는지 설명을 해보도록 하겠습니다.

 

 

 

 

1. 가설점정을 한다는 의미 (Comparison by box plot)

• 우리가 세운 가설이 옳다고 주장하기 위해서는 실험군과 대조군의 차이를 증명해야 합니다.
• 예를 들어, "운동이 간 수치 향상에 효과가 있다"라는 가설을 증명한다고 해보겠습니다.
• 우선 실험대상자를 30명 정도 선별하고 아래와 같이 실험을 진행했다고 해보겠습니다.
  • A group (실험군): 운동하기 전 간 수치 측정
  • B group (대조군): 운동한 후 간 수치 측정
• A, B group의 운동능력에 따른 간 수치 차이가 통계적으로 유의미한지 살펴봅니다.
• 보통 실험군에 대한 통계량과, 대조군에 대한 통계량을 box plot으로 표현하며, 이 둘 간의 차이가 유의미한지 시각화해줄 수 있습니다. (→ 어떻게 가설검정이 진행되는지는 가설검정 파트에서 설명하도록 하겠습니다.)

이미지 출처: https://www.datanovia.com/en/blog/how-to-add-p-values-onto-basic-ggplots/

 

(↓↓↓Box plot에 대한 설명↓↓↓)

https://89douner.tistory.com/200

[통계학]1. 통계학의 전체 구성도 (Feat. 기술통계, Box plot, 추론통계)

 

• 하지만, 위와 같이 30명만 선정하는 것이 문제가 되는 경우가 있습니다. 
• 앞선 예시를 기반으로 아래 두 가지 문제를 살펴보겠습니다..

 

1-1. 표본집단이 하나만 있을 때 발생하는 문제점 (1) - 양의 관점

• 가설검정을 통해 실험군과 대조군이 유의미한 차이를 보여 제가 세운 가설을 컨퍼런스에서 발표한다고 해보겠습니다.
• 그런데, A신문사 기자가 "실험군, 대조군에 속한 선별된 인원(=30명)만 비교한 것으로 우리나라 사람들에게도 똑같이 적용될 수 있을지 의문이다"라고 말합니다. → 즉, 선별된 표본 30명이 우리나라 국민전체인 모집단을 대표할 수 있느냐라는 질문입니다.
  • 예를 들어, 선별된 30명의 사람들 대부분이 운동직전에 간에 좋은 음식을 먹어서 간 수치가 좋아진 것일 수도 있죠. 그렇기 때문에, 또 다시 다른 사람들을 30명 선별해 운동을 시킨 후 간 수치를 측정해본다면, 간 수치가 크게 개선되지 않을 가능성도 있습니다. 

1-1. 표본집단이 하나만 있을 때 발생하는 문제점 (2) - 시간의 관점

• 이번에는 B신문사 기자가 "실험군, 대조군을 딱 한 번 실험해본걸로 충분한거냐?"라는 질문을 했다고 해보겠습니다.
  • 예를 들어, 실험을 했던 그 날 유독 실험군의 간 수치가 (운동을 통해) 개선된 것일 수 있습니다.
  • 즉, 다른 날에 했으면 실험군의 간 수치가 개선 개선되지 않을 가능성도 있다는 뜻이죠.

 

• 결국, 앞서 언급한 두 문제들이 좀 달라 보이지만 결국, 다수의 표본집단을 선별하는 것이 필요하다는 결론을 보여줍니다.
• Q. 그렇다면, 앞서 하나의 표본집단은 box plot으로 표현했는데, 다수의 표본집단들은 어떻게 표현하면 좋을까요? 다시말해, 다수의 표본집단들을 기반으로 어떻게 모집단을 표현할 수 있을까요? 이에 대한 답을 하기 위해 중심극한정리를 알아보도록 하겠습니다.

 

 

 

 

2. 중심극한 정리 (Central Limit Theorem))

• 중심극한 정리란 "모집단의 분포에 상관없이 표본크기가 커질수록 (적어도 30개 이상) 표본평균 \(\bar{X}\) 의 분포가 정규분포에 가까워진다는 이론"입니다.
• 예를 들어, 설명해 보겠습니다. (아래 그림(사진)과 같이 보시면 더 좋습니다.)
  • 우선 우리는 모집단의 분포를 모르는 상태입니다. (현실적으로 모집단을 파악하는건 불가능에 가깝습니다. 그래서, 통계학을 통해 표본을 추출하고 표본통계량을 기반으로 모집단과 관련된 모수들을 추정하는 것이죠)
  • 모집단의 분포를 파악하기 위해서 표본(집단)들을 추출합니다.
  • 개별적인 표본들(표본집단1, 표본집단2, ... 등)은 각각 별개의 확률분포를 갖고 있을 가능성이 큽니다.
  • 개별 표본들의 평균을 내면 표본평균의 분포를 구할 수 있다. (→ 표본평균 분포에 대한 개념은 우측 "링크"를 참고해주세요.)

 

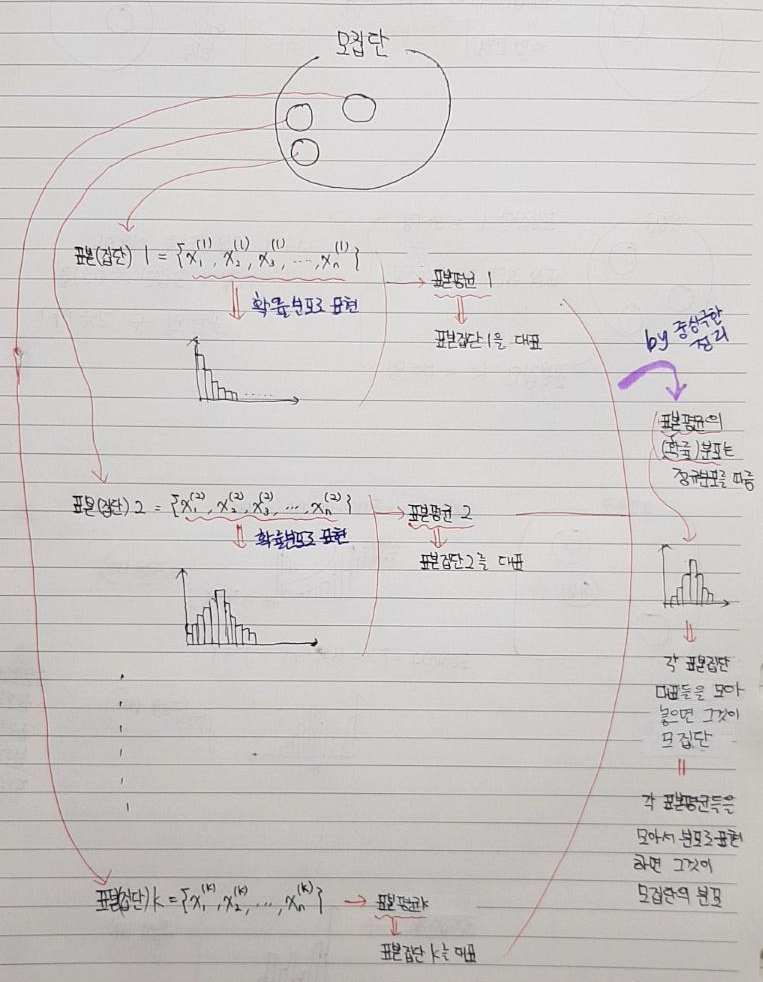
• 각각의 표본평균은 개별 표본집단을 대표하는 값입니다. 즉, 각각의 표본집단들의 대표를 모아두면 그것이 모집단을 상징한다고 가정할 수 있게됩니다. 

• 그래서, 표본집단들의 대표인 표본평균들을 확률분포로 표현하면 모평균의 분포가 됩니다.
• 중심극한정리에 따르면 표본(집단)크기가 커질 수록 (적어도 30개 이상) 표본평균의 분포가 정규분포에 가까워지기 때문에 모집단의 분포를 정규분포로 추론해볼 수 있습니다. → 통계학에서는 적어도 표본(집단)의 크기가 30개 이상이 되어야 한다고 합니다.
  • 표본의 크기 = 각 표본 집단에 속한 원소의 개수 = {x1, x2, ..., x3} 
  • 표본평균들의 평균이 모평균과 같다는 개념(→관련링크)과 같이 생각해봐도 좋을 것 같습니다 

 

(↓↓↓4:27초부터 시뮬레이션을 통한 직관적 설명↓↓↓)

https://www.youtube.com/watch?v=iTNHQXGIEuU 

 

 

[야구를 통한 중심극한정리 예시]

• 일반적인 현상을 통계로 나타낼 때, 대부분 평균주위에 많이 몰려있을 확률이 높습니다. 이는 중심극한정리를 통해 설명될 수 있습니다.
  • 예를 들어, 대한민국 프로야구 선발선수들의 직구 구속을 측정한다고 해보겠습니다.
  • 팀 당 선발투수의 직구 구속을 측정했다고 가정해보겠습니다.
    • LG는 선발진이 강해서 150대를 던진다고 해보겠습니다. (무적LG 만세!)
    • 삼성은 선발진이 리그 평균이라 대부분 140대를 던진다고 해보겠습니다.
  • 총 30개 팀들의 평균 구속을 산출한 후, 각 팀 평균들의 분포 (=표본평균 분포)를 나타냈더니 평균 140대이면서 정규분포를 구성하게 됩니다. (By 중심극한정리)
  • 즉, 프로야구 선발투수들의 투구들은 대부분 평균 140대일 것이고, 150대 투수들과 130대 투수들은 평균보다 적을 것이라고 추정해볼 수 있습니다. 

 

 

2-1. 표본의 크기가 충분히 크다면 중심극한 정리가 성립한다.

• 중심극한 정리를 공부하면서 가장 혼동되는 개념이 표본크기와 중심극한정리의 관계입니다.
• 앞서 설명한 것을 따르면, 표본크기가 적어도 30개 이상이고, 표본(집단)개수를 많이 추출해야 표본평균분포가 정규분포를 따른다고 보여집니다.
• 하지만, 아래 시뮬레이션을 보면 흥미로운 것이 표본크기인 n의 개수가 커질 수록, 표본(집단)개수(=Number of sampling)의 수가 줄어들어도 중심극한 정리가 형성되는 것을 볼 수 있습니다.

[시뮬레이션 예시]

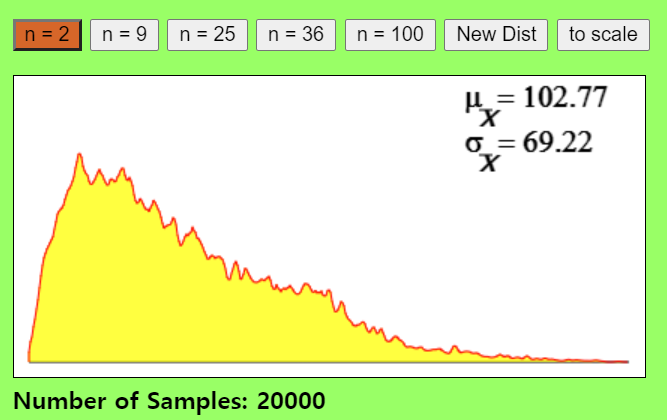
• 모집단이 지수분포를 따른다고 가정해보겠습니다.

 

• 모집단에서 표본크기2를 갖는 20000개의 표본(집단)개수를 추출하여 표본평균분포를 그리면 아래와 같습니다.

 

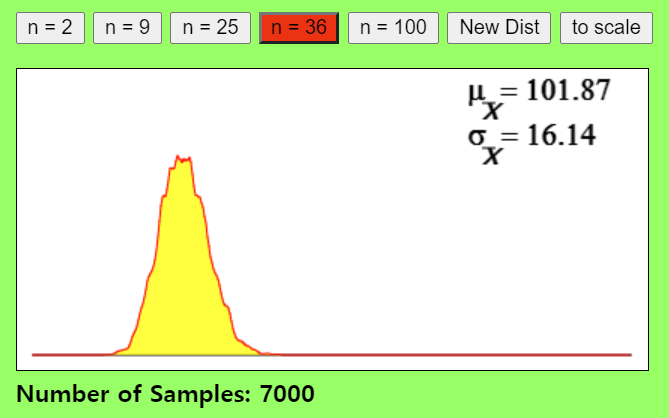
• 이번에는 표본크기를 36개로 늘려보겠습니다. 표본크기를 늘려보니 표본(집단)개수가 7000개만 돼도, 더욱 정교한 정규분포를 형성하는 것을 볼 수 있습니다.

 

• 표본크기가 100이 되면, 표본평균분포가 정규분포를 따르기 위해 필요한 표본(집단)수는 현격히 줄어들게 됩니다.

 

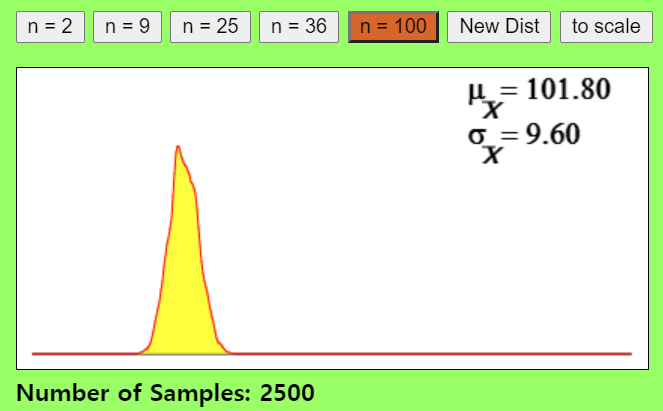
• 결국 표본크기가 충분히 크면 모집단으로 부터 추출하는 표본(집단)개수가 하나여도 정규분포를 이룰 수 있다는 추론이 가능해집니다.
• 개인적으로 생각했을 때는 결국 모집단으로부터 추출되는 표본의 총 수는 "표본크기×표본(집단)개수"가 되기 때문이 아닐까 싶습니다. 즉, 표본(집단)개수가 하나여도 표본크기가 엄청 크다보면 모집단의 평균에 해당하는 원소들이 가장 많이 추출이 될 것이기 때문입니다 (=자연스럽게 모집단 평균이 아닌 원소들이 선별되는 횟수가 점점 줄어들겠죠)

이미지 출처: https://m.blog.naver.com/mykepzzang/220851280035

이미지 출처: https://m.blog.naver.com/mykepzzang/220851280035

 

 

 

(↓↓↓중심극한정리 시뮬레이션 싸이트↓↓↓)

http://www.ltcconline.net/greenl/java/Statistics/clt/cltsimulation.html

 

 

 

 

 

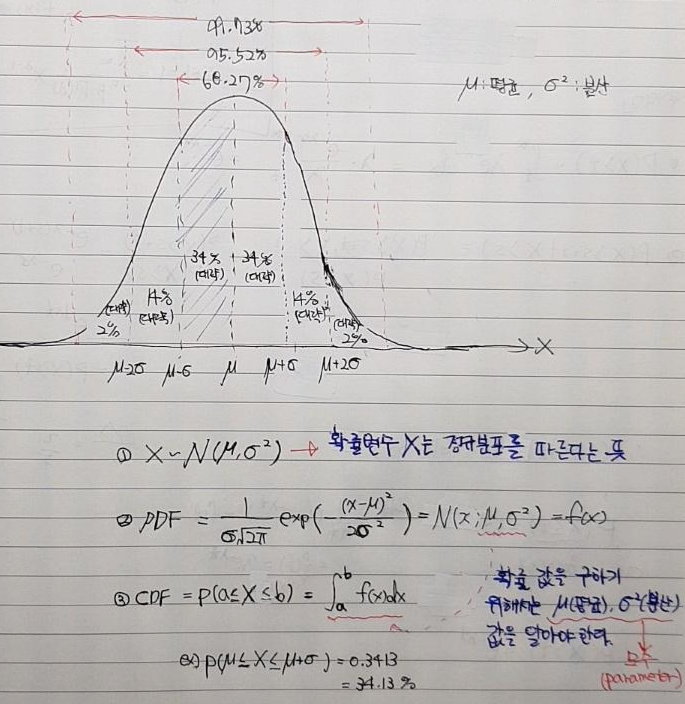
3. 정규분포(Normal distribution = Gaussian distribution)의 수학적 의미(정의) 

• 앞서 중심극한 정리를 통해 아래와 같은 이야기를 할 수 있다고 했습니다.

 

"일반적인 현상을 통계로 나타낼 때 대부분 평균 주위에 가장 많이 몰려있고, 그 수치가 평균보다 높거나 낮은 경우 정규분포를 따른다고 합니다. "

 

• 그렇다면, 정규분포의 수학적인 정의는 어떻게 될까요?
• 정규분포는 영어로 normal distribution이라고 하는데, 가우스가 이러한 확률분포를 처음 발견했기 때문에 Gaussian distribution이라고 부르기도 합니다.

 

 

 

 

 

 

4. Parameterized by precision

• 분산 값을 통해 알 수 있는 사실은 데이터들이 평균 보다 얼마나 멀리 떨어져 있는지 알 수 있습니다.
• 하지만, 몇몇 사람들은 precision이라는 개념이 분산(variance)보다 더 직관적(intuitive)일 수 있다고 합니다.
• 그 이유는, precision 값을 이용하면 평균 주위에 값들이 얼마나 많이 몰려있는지 알 수 있는데, 대부분의 경우 데이터들이 평균으로 부터 얼마나 떨어져 있는지 보다는 평균 주위에 얼마나 몰려있는지를 파악하는게 더 유용할 때가 있기 때문입니다.
• Precision(=\(\beta\))은 분산의 반비례 입니다. 

 

 

 

 

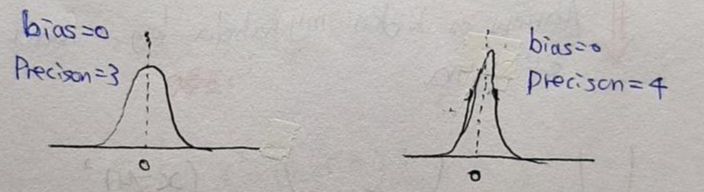
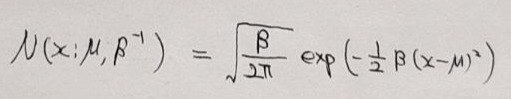
5. Normal distribution 수식 도출

• 수식 유도는 아래 영상을 참고하시면 될 것 같습니다.

 

https://www.youtube.com/watch?v=sFMjrnI93b4 

 

 

 

 

6. 정규분포 With 엑셀

실제 연구나 현업에서는 정규분포를 어떻게 구하는지 엑셀을 통해 간단히 알아보겠습니다.

• 먼저, 우리에게 어떤 데이터들이 주어져 있다고 합시다.
• 그럼 이러한 데이터들을 통해 평균, 분산, 표준편차 값을 구할 수 있을 겁니다.

(↓↓↓엑셀을 이용한 정규분포 구하는 방법↓↓↓)

https://www.youtube.com/watch?v=Ke0uCHgAYJw 

 

 

 

 

 

 

 

7. 정규분포의 활용 (Feat. 가설검정)

• 지금까짖 정규분포를 배운 이유는 "우리가 세운 가설을 검정(testing)하는데 유용한 도구로 사용"되기 때문입니다.
• 이 부분에 대한 자세한 설명은 '가설검정' 파트에서 설명드리도록 하겠습니다.

(↓↓↓중심극한정리 설명과 이것이 가설검정에 쓰이는 예시를 간단하게 보여주는 영상↓↓↓)

https://www.youtube.com/watch?v=YAlJCEDH2uY 

 

이미지 출처: https://yeomko.tistory.com/37

 

이미지 출처: https://techntalk.tistory.com/entry/%EB%B0%95%EC%8A%A4%ED%94%8C%EB%A1%AF-Box-Plot%EA%B3%BC-%EC%A0%95%EA%B7%9C%EB%B6%84%ED%8F%ACnormal-distribution%EC%9D%98-%EA%B4%80%EA%B3%84-%EB%B0%95%EC%8A%A4%ED%94%8C%EB%A1%AF-%EA%B7%B8%EB%A6%AC%EB%8A%94-%EB%B2%95