안녕하세요.
이번글에서는 일(1)표본(=단일표본) T검정에 대해서 알아보도록 하겠습니다.
[가설검정의 종류]
- '차이'와 관련된 검정
- '평균'의 차이를 검정 하고 싶을 때
- 1-1. 비교하는 집단이 하나일 때
- 1-1-1. 모분산을 알고 있는 경우
- 일(1)표본 Z 검정 (One-sample Z test) → ex) 귀무가설(\(H_{0}\)): 한국의 평균은 K이다.
- 1-1-2. 모분산을 모르는 경우
- 일(1) 표본 T 검정 (One-sample T test) → ex) 귀무가설(\(H_{0}\)): 한국의 평균은 K이다.
- 1-1-1. 모분산을 알고 있는 경우
- 1-2. 비교하는 집단이 둘일 때
- 1-2-1. 모분산을 알고 있는 경우 & 표본이 클 때
- 이(2)표본 Z 검정 (Two-sample Z test) → ex) 귀무가설(\(H_{0}\)): 남, 녀간의 평균에 차이가 없다.
- 1-2-2. 모분산을 모르는 경우 & 표본이 작을 때
- 1-2-2-1. 독립표본 T 검정 (Independent Sample T test) → ex) 귀무가설(\(H_{0}\)): 남, 녀간의 평균에 차이가 없다.
- 1-2-2-2. 대응표본 T 검정 (Paired Sample T test) → ex) 귀무가설(\(H_{0}\)): 남, 녀간의 평균에 차이가 없다 & 해당 차이를 반복해서 검증 (한 달간 간격을 두고 측정: 1개윌 뒤, 2개윌 뒤, 3개윌 뒤, ....)
- 1-2-1. 모분산을 알고 있는 경우 & 표본이 클 때
- 1-3. 비교하는 집단이 셋 이상일 때
- 1-3-1. ANOVA (분산분석)
- 1-3-1-1. 일원 분산분석 (One-way ANOVA) → ex) 귀무가설(\(H_{0}\)): 한국, 미국, 독일의 평균에 차이가 없다
- 1-3-1-2. 반복측정 분산분석 (Repeated Measures ANOVA) → ex) 귀무가설(\(H_{0}\)): 한국, 미국, 독일의 평균에 차이가 없다 & 해당 차이를 반복해서 검증 (한 달간 간격을 두고 측정: 1개윌 뒤, 2개윌 뒤, 3개윌 뒤, ....)
- 1-3-1-3. 이원 분산분석 (Two-way ANOVA) → ex)
- 1-3-1-4. 이원반복측정 분산분석 (Two-way Repeated Measures ANOVA) → ex)
- 1-3-1. ANOVA (분산분석)
- 1-1. 비교하는 집단이 하나일 때
- '평균'의 차이를 검정 하고 싶을 때
1. 일(1)표본 T검정 (One-sample T-test) = Student T-test
- 일(1)표본 T검정은 다음 아래와 같은 상황에서 진행되는 가설검정 방식입니다.
- 한 집단의 평균을 검정(test)하고 싶은 경우
- 해당 집단의 (모)평균은 알고 있지만, (모)분산을 모르고 있다고 가정할 경우
- 귀무가설(\(H_{0}\)): 표본평균과 모집단 평균을 같다.
- 대립가설(\(H_{1}\)): 표본평균하고 모집단 평균은 차이가 있다.
- ex) 전국학교의 평균성적과 우리학교의 평균성적은 같은가?
- 또한, 일(1)표본 T검정은 정규분포를 가정하기 때문에, 표본크기가 30개 이상있을 때를 전제하고 있습니다 (By 중심극한 정리)
- 일표본 T검정은 william이라는 사람이 발명했는데 당시 william의 필명이 student라고 해서, student T검정이라고도 부릅니다.
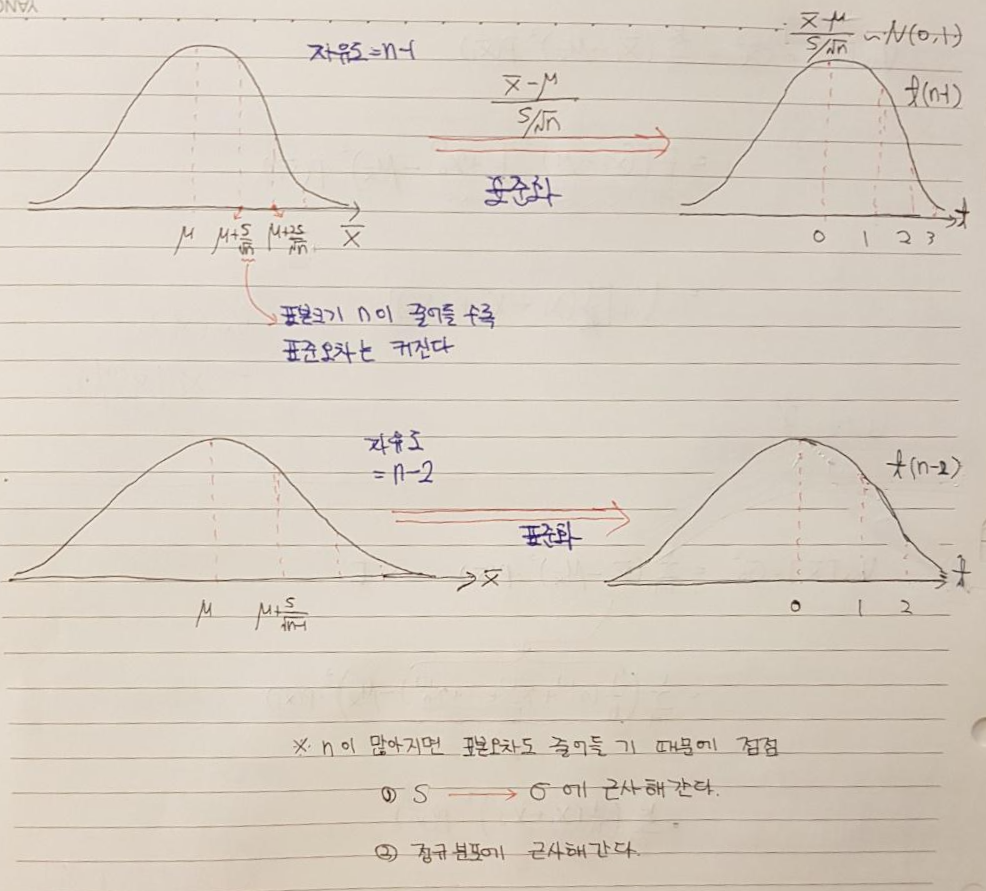
1-1. 표준오차
- 일표본 T검정을 이해하기 위해 반드시 알고 있어야 할 개념이 표준오차입니다.
- 그렇기 때문에 표준오차에 대한 설명을 조금 해보도록 하겠습니다.
- 표준오차
- 표본평균의 분산에 루트를 씌워준 것
- 의미상으로 표본오차를 접근할 때는 표본평균의 분산의 의미로 생각하면 됨
- 표본평균의 분산: 표본평균들이 표본평균들이 표본평균들의 평균으로부터 얼마나 떨어져 있는지 알려주는 척도
(↓↓↓표본평균의 평균, 표본평균의 분산과 관련된 설명↓↓↓)
https://89douner.tistory.com/188?category=985452
[통계학]2-1.표본 통계량(표본평균, 표본분산, 자유도, 표본분포)
표안녕하세요. 지난 글에서 통계학에 대한 제 개인적인 정의를 내린바 있습니다. "나의 주장(가설)을 보편 타당하게 증명하는 과정" 가설설정(Statistical hypothesis setting) = 내가 주장하려고 하는
89douner.tistory.com

1-2. Z분포와 T분포의 차이
(↓↓↓Z분포, Z검정 설명↓↓↓)
https://89douner.tistory.com/202?category=985452
[통계학]4-1-1. 한 집단의 평균을 검정(test)할 때 (Feat. 일표본(단일표본) Z검정, 신뢰구간, 단측검정
안녕하세요. 이번 글에서는 한 집단의 평균을 검정(test)하는 두 가지 가설검정 방식중 하나인 일(1)표본(=단일표본) Z검정에 대해 알아보도록 하겠습니다. 일(1)표본(=단일표본) Z검정 (One-sample Z tes
89douner.tistory.com
(↓↓↓표본평균의 (확률)분포↓↓↓)
https://89douner.tistory.com/188
[통계학]2-1.표본 통계량(표본평균, 표본분산, 자유도, 표본분포)
표안녕하세요. 지난 글에서 통계학에 대한 제 개인적인 정의를 내린바 있습니다. "나의 주장(가설)을 보편 타당하게 증명하는 과정" 가설설정(Statistical hypothesis setting) = 내가 주장하려고 하는
89douner.tistory.com

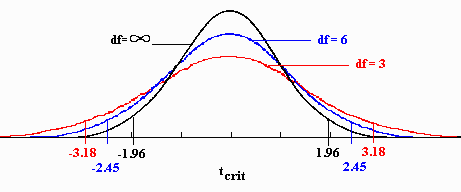
- 양측검정을 해야하는 경우라면 해당분포 양측 5%에 해당하는 critical value(임계값)을 설정해주어야 합니다.
- 주의해야 할 점은, t분포는 자유도에 따라 양측 5%에 해당하는 critical value 값들이 다르다는것을 유의해야 합니다.

2. 일(1)표본 T검정 (One-sample T-test) 예시
- 전국 대학교 대학생 평균 키 = 178.5
- 우리 대학교 대학생 평균 키 = 179.9
- 귀무가설: 전국 대학교의 대학생 평균 키와 우리 대학교 대학생 평균 키는 (통계적으로) 같다고 할 수 있다.
- 대립가설: 전국 대학교의 대학생 평균 키와 우리 대학교 대학생 평균 키는 (통계적으로) 다르다고 할 수 있다.
- 우리 대학교 대학생 키 표준편차(s) = 표본표준편차(s) = 7.05
- 표본크기(n) = 101
- 자유도 = n-1 = 100
- 임계값 = 1.984 ← T분포의 임계값은 아래 그림처럼 T-table을 참고하면 됩니다. 아래 그림에서 95%신뢰수준, 자유도 100, 양측검정일 경우 임계값은 1.984 입니다.
(↓↓↓신뢰수준과 기각역에 대한 설명↓↓↓)
https://89douner.tistory.com/202
[통계학]4-1-1. 한 집단의 평균을 검정(test)할 때 (Feat. 일표본(단일표본) Z검정, 신뢰구간, 단측검정
안녕하세요. 이번 글에서는 한 집단의 평균을 검정(test)하는 두 가지 가설검정 방식중 하나인 일(1)표본(=단일표본) Z검정에 대해 알아보도록 하겠습니다. 일(1)표본(=단일표본) Z검정 (One-sample Z tes
89douner.tistory.com

- t-value는 기각역에 포함하므로 대립가설을 채택합니다. → 즉, T검정 결과 "전국 대학교의 대학생 평균 키와 우리 대학교 대학생 평균 키는 (통계적으로) 다르다"고 할 수 있습니다.

(↓↓↓위의 예제 유튜브 링크↓↓↓)
https://www.youtube.com/watch?v=EzH5n31Com0&list=PLalb9l0_6WArHh18Plrn8uIGBUKalqsf-&index=5
3. 일(1)표본 T검정 (One-sample T-test) 엑셀적용 예시
- 아래 영상에서 Dummy sample을 두는 이유는 아래와 같습니다.
- T검정의 귀무가설은 "표본평균=모평균" 설정한 상태이다.
- 또한 모집단의 분산 (모분산)을 모른다고 가정한다.
- 즉, 모집단에 대한 데이터들이 없어도 되기 때문에, 모집단에 대한 데이터가 없어도 된다. → 그래서 아래 영상에서 dummy column을 만든다.
- 결과적으로, 표본데이터들만 있어도 T검정이 가능하다.
https://www.youtube.com/watch?v=v-ZcqrdTcIQ
'딥러닝수학 > 확률-통계학' 카테고리의 다른 글
| [통계학]4-2-1. 두 집단의 평균 차이를 검정(test)할 때 (Feat. 독립표본 Z검정=이(2)표본 Z검정) (0) | 2021.05.30 |
|---|---|
| [통계학]4-1-1. 한 집단의 평균을 검정(test)할 때 (Feat. 일표본(단일표본) Z검정, 신뢰구간, 단측검정(One-tailed test), 양측검정(Two-tailed test)) (0) | 2021.05.27 |
| [통계학-가설검정] 4.가설의 종류를 파악하기 (Feat. 귀무가설, 대립가설) (2) | 2021.05.26 |
| [통계학]3.정규분포를 따른다는 의미 (Feat. 중심극한정리) (0) | 2021.05.26 |
| [통계학]2-2.표본통계량(공분산, 상관계수) (0) | 2021.05.25 |