Time Traveler

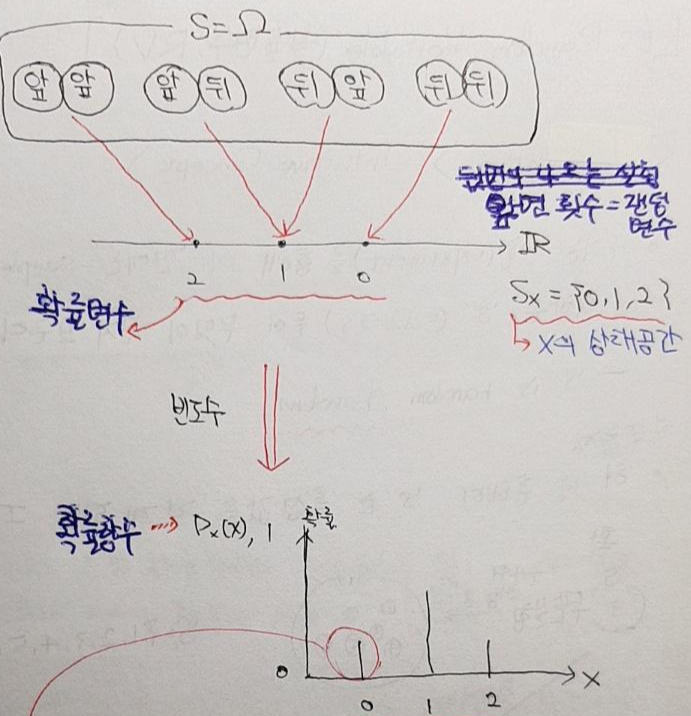
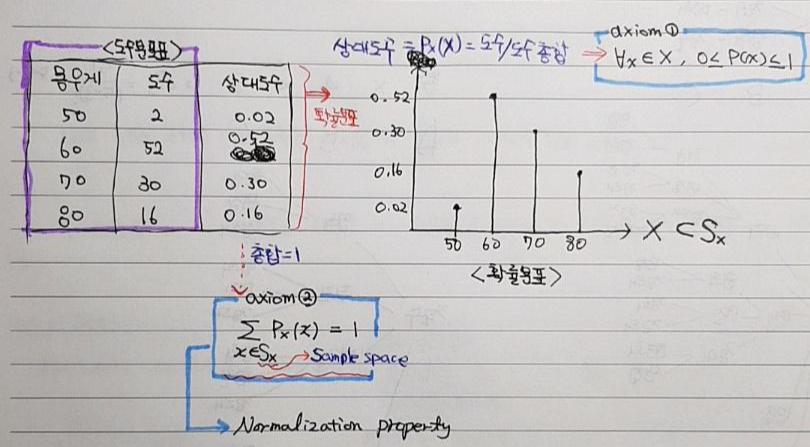
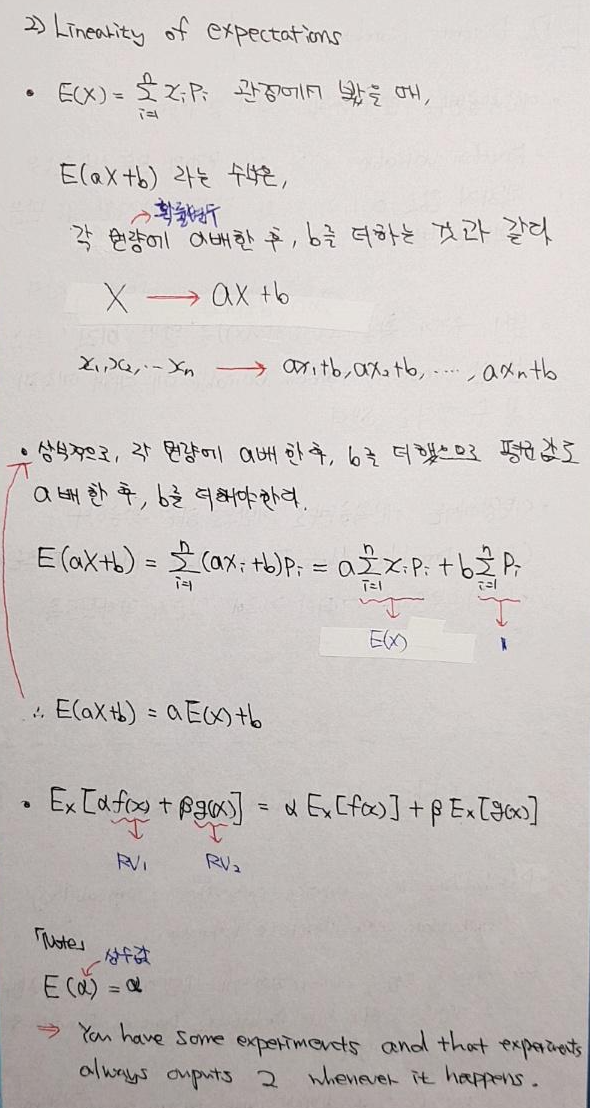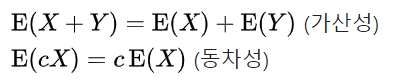[이번 장에서의 목표]

• 이번장에서는 이산확률변수를 기반으로 한 다양한 확률분포들에 대해서 알아보도록 하겠습니다.
• 앞서 확률분포와 평균, 분산을 구하는 방법에 대해서 알아보았으니, 이번장에서는 각각의 확률분포가 어느 경우에 사용되는 건지, 해당 확률분포의 평균과 분산은 어떻게 되는건지 알아보도록 하겠습니다.

1. Cumulative Distribution (누적확률분포)

• 누적확률분포는 말 그대로 특정 확률변수까지 누적된 확률 값을 알아내기 위해 사용됩니다.
• 예를들어, 확률변수 3이전의 경우(1,2,3)가 나올 확률에 대해서 알아보는 것과 같습니다.

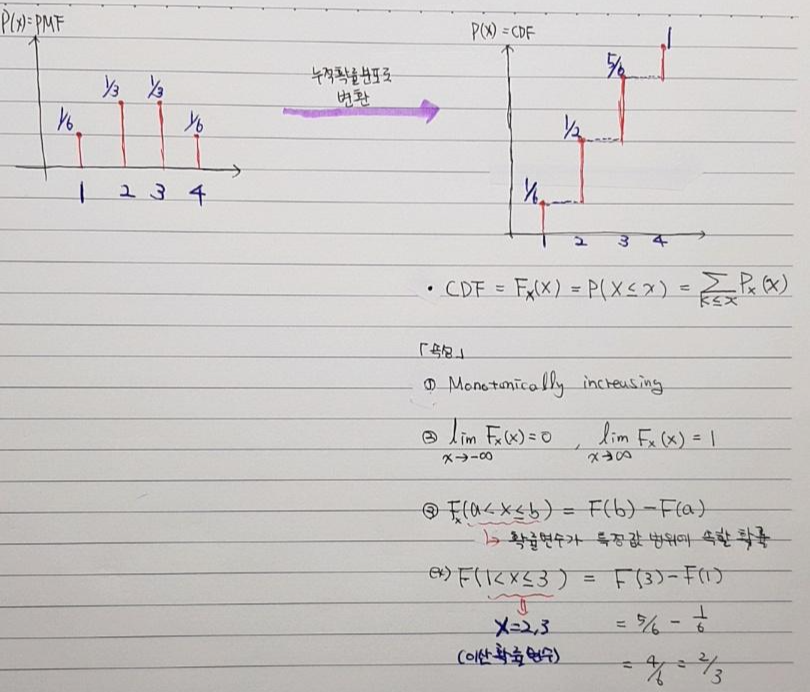
• 모든 확률분포는 PMF 또는 CDF로 표현 가능합니다.

2. Bernoulli Distribution (베르누이 확률분포)

2-1. 베르누이 확률함수

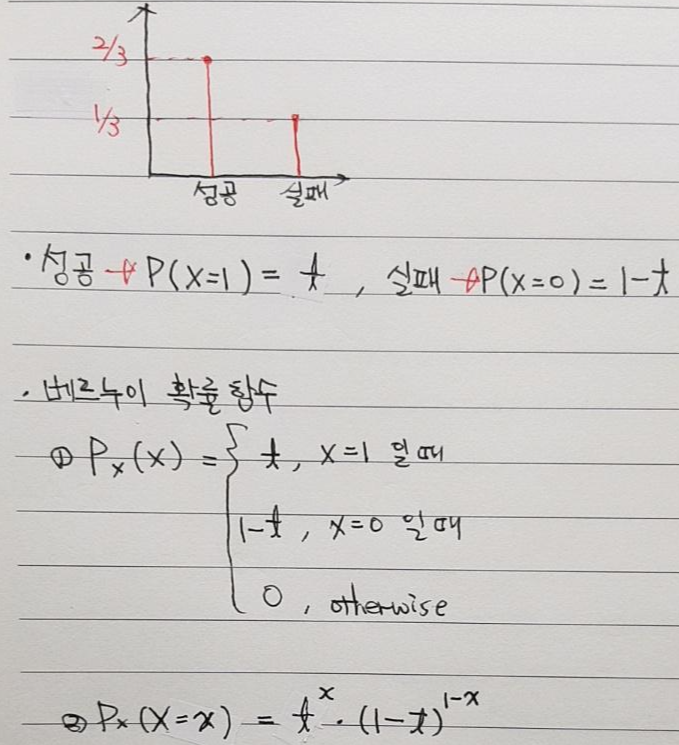
• 베르누이 분포는 성공과 실패 또는 이분법적인 상황에 대한 확률 값을 나타내고자 하는 확률분포입니다.
• 즉, 베르누이 분포에서 확률 변수는 2가지 만 존재하고, 이 두 가지의 확률값은 p, 1-p 입니다.

2-2. 베르누이 확률분포의 평균식 증명

2-2. 베르누이 확률분포의 분산식 증명

3. Binomial Distribution (이항확률분포)

3-1. 이항확률 함수

• 이항확률함수는 n번 실행했을 때 x번 성공할 경우에 대한 확률 값을 도출합니다. 이 때, x번 성공하는 횟수가 이항확률함수의 (Binomial) random variable이 됩니다. 예를 들어, 100번 동전을 던졌을 때 앞면이 50번 나올 확률을 구할 때 사용되는 함수입니다.
• Binomial random variable is Independent Identically Distribution (I.I.D) Bernoulli. (독립시행 링크)
  • 시행(trial)이 연속적일 때, 이전 시행의 결과가 다음 시행에서 일어날 확률에 아무런 영향을 미치지 않습니다. (Independent)
  • 시행할 때마다 항상 성공과 확률이 같은 bernoulli distribution을 따릅니다 (Identically Distribution)
  • Binomial distribution은 독립시행 확률을 따르는 I.I.D라고 할 수 있습니다.
• 종합하자면, Bernoulli random variable을 따르는 bernoulli experment를 n번 실행하여 성공횟수를 binomial random variable로 삼는 확률분포를 binomial distribution이라 합니다.
• 이항분포는 아래와 같은 확률함수를 갖는다. (해당 확률함수의 증명은 아래 예시를 보면 직관적으로 파악할 수 있습니다)

(조합 관련 개념 또는 아래의 예시에 대한 자세항 설명은 다음 링크에서 독립시행 확률 part을 참조해주세요)

2-2. 베르누이 확률분포의 평균식 증명

2-3. 베르누이 확률분포의 분산식 증명

4. Geometric Distribution (기하분포, 연속확률변수에서는 지수분포가 됨)

4-1. 기하분포 확률함수

• Geometric distribution의 random variable은 성공할 때 까지 시행한 횟수를 의미합니다.

(↓↓↓위에 무한 등비급수합 수식증명↓↓↓)

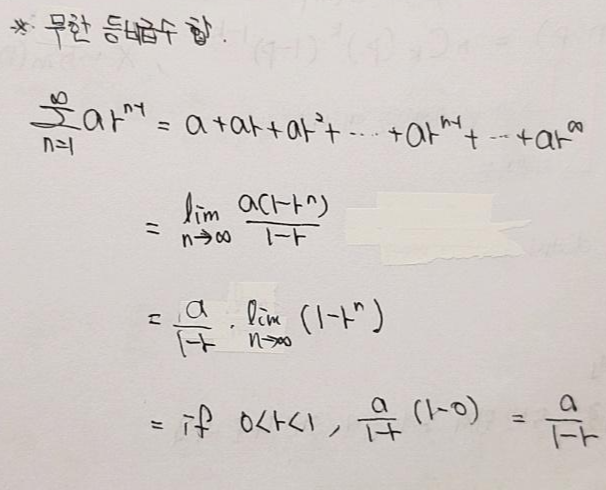
4-2. 기하분포 확률분포의 평균식 증명

• 왜 해당 시그마 공식이 1/p^2 를 도출하는지 증명하겠습니다.
• 먼저 등비수열 공식에 따라 아래와 같이 정의할 수 있습니다.

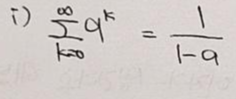
• 해당 등비수열 공식을 양쪽으로 미분해보겠습니다.

• 이로써 평균 수식의 증명이 완료되었습니다.

4-3. 기하분포 확률분포의 분산식 증명

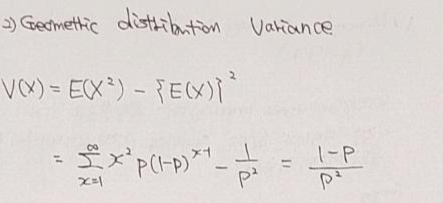
• 기하확률분포의 분산식 증명은 아래와 같습니다.

4-3. Memoryless property in Geometric distribution (무기억성 성질)

• 위의 식에 대한 이해을 위해 몇 가지 예시를 들어보겠습니다.
• [첫 번째 예시]
  • P(X>t)라는 뜻은 t번 시도한 후에 3점 슛을 성공할 확률을 의미합니다.
  • 농구를 좋아하는 학생이 3점 슛을 성공하기 위해 s번의 실패(시도)를 했다고 합시다. 그리고 t번의 실패(시도)를 더 한 끝에 슛을 성공했습니다. 그리고 s+t번 이후에는 계속해서 슛을 성공시킵니다. 이를 조건부 확률로 표현하자면 P(X≥s+t | X≥s) 입니다.
  • 사실 위에서 설명한 개념들을 P(X≥s+t)만으로도 설명 가능한거라고 볼 수 도 있는데, 조건부 개념을 도입한건 무기억성이라는 특성을 설명하기 위해서 인듯합니다 (즉, 위의 수식을 만족하기 위해 도입한 개념). 그럼, 계속해서 알아보도록 하겠습니다.
  • P(X≥s+t | X≥s) = P(X≥t) 수식을 보면 s번의 시도를 한 후에 t번 더 시도해서 성공할 확률과, t번 시도해서 성공할 확률과 같다는 뜻이됩니다. 
  • 즉, s+t번의 시도를 한 것 과, t번의 시도를 한 것을 동일하게 보는 것인데, 예를 들어,s=5, t=2라고 했을 때 단순히 5+2(=s+t)번의 시도와 2(=t)번의 시도가 같다고 보는게 아니라, 5번의 시도를 어떻게 바라볼 것인가가 포인트가 될 수 있다고 생각합니다. 어떻게 보면 s번 시도 한것은 농구를 좋아하는 학생이 집중을 못했기 때문에 아무 의미가 없었다는 결론을 내릴 수도 있을 것 같습니다.
  • 결과적으로, s번의 실패(시도)가 아무 의미 없어진 것과 같습니다. 즉, s번의 실패(시도)에 대한 기억을 잃어버리게 되는 것이죠. 
• [두 번째 예시 - 링크] (해당 예시는 좌측 링크 사이트에서 인용했습니다)
  • 어떤 기계가 처음 만들어져서 사용되기 시작한 뒤 t시간 이내에 고장날 확률과, 그 기계가 s시간 까지 계속 사용되다가 t시간 이내에 고장날 확률이 동일하다는 말과 같습니다.
  • 기계가 이전 s시간 동안 사용되었다는 것을 기억하지 못하는 것과 같습니다 (무기억).
• 위의 예시를 통해 봤듯이, 무기억성이란 특정분포가 과거의 이력을 잊어버리는 성질을 의미합니다. 이력을 잃어 버리더라도 특정 분포를 여전히 따릅니다. 
• 그렇다면 무기억성의 수식을 증명해보도록 하겠습니다.

4-4. 기하분포 어원

• 기하확률분포의 확률함수는 등비수열이라고 할 수 있는데, 왜 등비수열에 geometric이라는 표현을 사용했을까요?

5 Negative Binomial Distribution (음이항분포 or Pascal distribution)

5-1. 음이항분포 확률함수

• r번의 성공횟수를 기록할 때 까지 x번 실패 할 횟수를 random variable로 갖는 확률분포입니다. 즉, r번 성공할 때 까지 x번 실패 하는 경우에 대한 확률값을 알고자 할 때 사용하는 확률함수가 음이항분포 확률함수입니다.  
• 여기서 중요한 부분은 r은 고정 값이고, x는 random variable이기 때문에 변할 수 있는 변수이고, n=x+r이기 때문에 x에 따라 n(시행) 값이 변합니다.
• 먼저 예를 통해 설명해보도록 하겠습니다. 
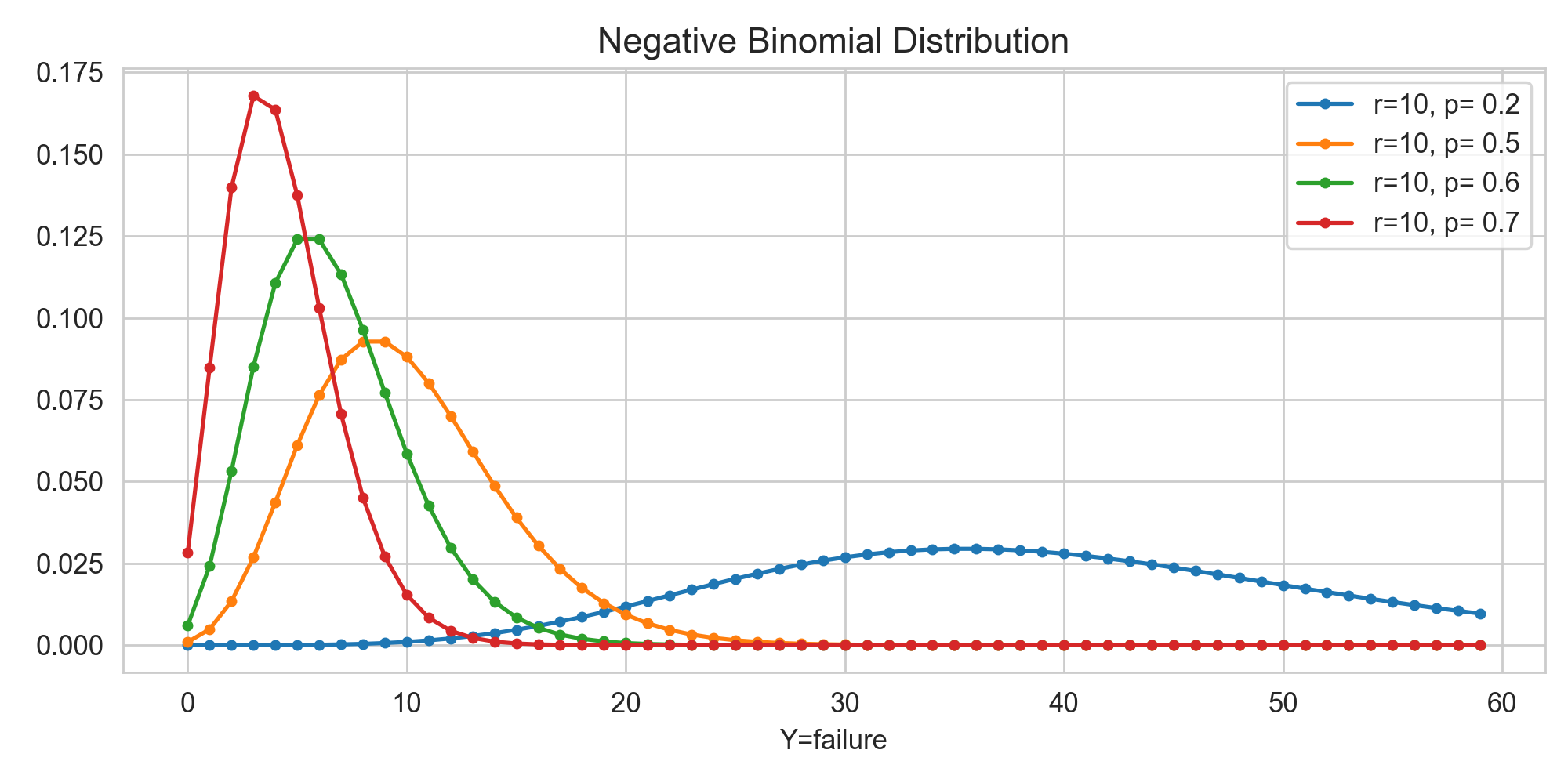
• 아래 예를 보면, 3번 성공하는 동안 실패하는 횟수에 따라 확률값을 알고자 합니다. 먼저, 3번 성공할 때까지 1번 실패할 확률을 구하는 과정은 아래와 같습니다. (음이항확률함수=P(X))먼저, 음이항분포를 표현하기 위해서는 성공횟수(r)가 고정되어 있어야 합니다. 실패횟수(x)가 random variable이기 때문에 시행횟수 (n=r+x)도 실패횟수에 따라 변경됩니다.

• 예를 들어, 아래 표에서 성공횟수는 10으로 고정되어 있고, 시행횟수는 보이지 않지만 implicit (암묵적)으로 실패횟수에 따라 변한다고 보시면 됩니다. 만약 아래 실패횟수(random variable)가 60이 최대치라면, 전체 시행횟수(n=x+r)는 70이 됩니다.)

5-2. 음이항분포의 평균식 증명

• 평균수식을 알아보기 전에 음이항분포에서의 모든 확률 값의 총합이 1임을 확인해보겠습니다.

• 지금부터 평균 식을 증명해보겠습니다.

5-3. 음이항분포의 분산식 증명

5-4. 음이항분포와 기하분포의 관계

• 음이항분포를 자세히 보면 r=1일 때 기하분포와 동일하다는 것을 확인할 수 있습니다. 즉, 성공횟수가 1이 나올 때 까지 시행한 횟수를 확률 변수를 삼는다는 것은 성공할 때까지 시행한 횟수를 확률변수로 삼는다는 것과 같습니다. 즉, 기하분포의 정의인 "성공할 때까지 시행한 횟수를 random variable로 삼는다"와 동일한 경우라고 볼 수 있습니다. 그러므로, 기하분포는 음이항분포의 특이한 케이스라고 보시면 될 것 같습니다.
• 식으로 증명하면 아래와 같습니다.

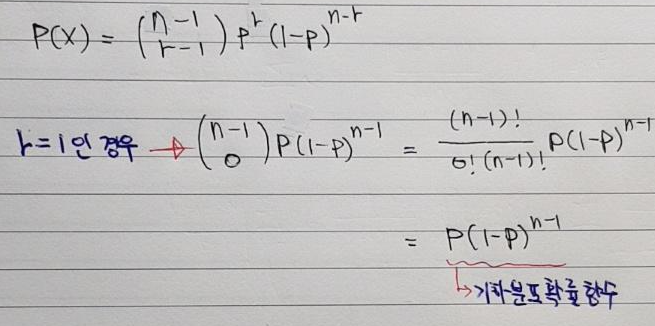
6. Hypergeometric Distribution (초기하 확률분포)

6-1. 초기하분포 확률함수

• 초기하분포 역시 이항분포와 마찬가지로 '성공', '실패' 2가지 상황만 나오는 실험에서 사용됩니다.
• 하지만, 이항분포와 복원추출인 반면에 초기하분포는 비복원추출을 전제로 합니다. 
• 결국, 현재 진행하는 실험의 sample space(표본공간)가 이전 실험의 sample space보다 작기 때문에 이전실험이 현재실험의 확률값에 영향을 미치게 됩니다. 그러므로, 초기하분포는 다음과 같은 의미를 내포합니다 → "Non-independent Bernoulli trials"
• 아래 수식은 초기하분포 확률함수 수식입니다. 이에 대해서 설명해보도록 하겠습니다. 

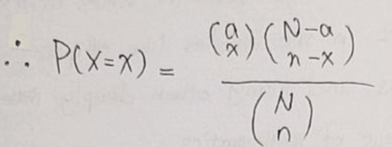
• 초기하분포의 수식은 모집단과 표본에 대한 개념을 베이스로 두고 있습니다. 두 측면에서 초기하분포를 설명해보도록 하겠습니다.
  • [첫 번째 설명]
    • 모집단의 크기를 N이라고 하고, 모집단 안에는 우리가 원하는 원소가 a개 있다고 하겠습니다.
    • 모집단에서 크기가 n인 표본을 뽑습니다.
    • 해당 표본안에서 우리가 원하는 원소가 x개 있을  확률분포를 초기하확률분포라고 합니다.
    • 즉, 표본안에서 우리가 원하는 원소가 뽑히는 갯수 (x)가 random variable이 됩니다.
  • [두 번째 설명]→ 두 번째 설명은 우측 사이트를 참고했습니다 링크
    • N개의 구성원의 모집단이 있습니다.
    • 이 모집단이 두 그룹으로 나누어진다고 가정하겠습니다. 
    • 첫 번째 그룹에는 a개의 구성원이 있다고 하면, 두 번째 그룹에는 N-a개의 구성원이 존재합니다.
    • 이때 초기하 확률변수 x는 전체 모집단에서 n개의 샘플을 비복원으로 뽑을 때, n개 샘플 중에서 첫 번째 그룹(=a)에 해당하는 샘플 수를 의미합니다.
  • [예시]
    • 하나의 상자에 6개의 빨간색 공과, 14개의 노란색공이 있습니다.
    • 비복원으로 5개의 공을 추출합니다.
    • 이때 5개의 공 중 4개의 공이 빨간색일 확률은 얼마입니까?

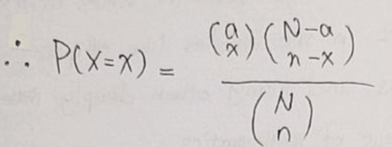
6-2. 음이항분포의 평균식 증명

6-3. 음이항분포의 분산식 증명

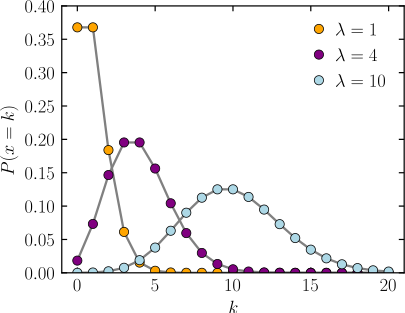
7. Poisson Distribution

• 포아송 분포는 '단위시간(or공간)안에 어떤 사건이 몇 번 발생할 것인지를 표현하는 이산 확률 분포입니다.
  • 한 달 동안 발생하는 교통사고의 횟수
  • 책 한 페이지 당 오타의 횟수 → 예시 인용 사이트 링크
    • 어느 전공 책 5페이지를 검사했는데, 10개의 오타가 발생했다. 이 책에서 어느 한 페이지를 검사했을 때, 오타가 3개 나올 확률은?
• 포아송 분포에서의 발생하는 사건의 횟수가 random variable이 되고, 발생하는 평균 횟수가 고정값(=\(\lambda\))이 됩니다. 발생하는 평균횟수는 "전체 시행횟수×사건이 발생할 확률"입니다. (위의 예시를 기준으로 값을 설정해보겠습니다)
  • 사건이 발생하는 횟수=k→ 3
  • 전체 시행횟수=n→ 5
  • 사건이 발생할 확률=p=\lambda/n → (10/5)/5
  • 특정 시행횟수에서 사건이 발생할 수 있는 평균 횟수= \(\lambda\)=n×p
• 위의 전공 책 관련 예시를 보면, 3건의 사건이 발생할 횟수 (오타가 나올 횟수=3) 가 random variable이 되고, 이러한 경우 (random variable=3)의 확률을 알아보기 위해, 한 페이지 당 오타가 발생할 평균 횟수 \(\lambda\)=10/5 을 알고 있어야 합니다. (여기에서는 성공할 확률을 딱히 몰라도 \(\lambda\)=2 이라는 건 알 수 있습니다.
• 우리는 "어느 전공 책 5페이지를 검사했는데, 10개의 오타가 발생했다."에 대한 정보를 기반으로, "어느 한 페이지를 검사했을 때, 오타가 3개 나올 확률은?"에 대한 답을 해야합니다.
  • 어느 한 페이지라는 것은 단위공간이라고 볼 수 있고, 이것을 전체 시행 횟수(=n)로 볼 수 있습니다. 
  • 결국 이는 한 페이지에 n이라는 글자가 있다면, 거기서 k개의 오타가 나올 확률을 의미하고, 이를 다른 측면에서보면 n번 동전을 던졌을 때 k번 앞면이 나올 확률과 동일한 문제가 됩니다. 즉, 이항확률분포(Binomial distribution)의 확률 함수와 동일 한 것이죠.
  • 포아송 분포에서 중요한 전제조건은 n이 굉장히 크다는 상황을 가정하고 있다는 것입니다. 즉, 이항확률분포에서 n이 엄청크다면 포아송 분포로 근사할 수 있다는 의미입니다. 이러한 방식을 사용했던 이유는, 과거에 계산기가 없었을 때 n이 엄청 크다면 이항확률분포를 계산하는게 엄청 힘들었기 때문에 n이 무한대라는 극한의 개념을 도입해 포아송 확률함수를 만들었다고 합니다. 즉, 이항확률분포에서 n이 굉장히 큰 경우 포아송 분포식으로 계산할 수 있게 되는 것이죠 (근래에는 컴퓨터의 발달로 이항확률분포 n이 충분히 커도 쉽게 계산 가능하다고 하지만, n>50, or \(\lambda\)=np<5 이면 컴퓨터에서 비트의 제한으로 수치에러가 날 경우가 있다고 합니다.)
  • 그럼 지금부터 n이 무한대일 때 이항분포 확률함수가 어떠한 확률 함수를 갖는지 살펴보도록 하겠습니다.

①식 풀이

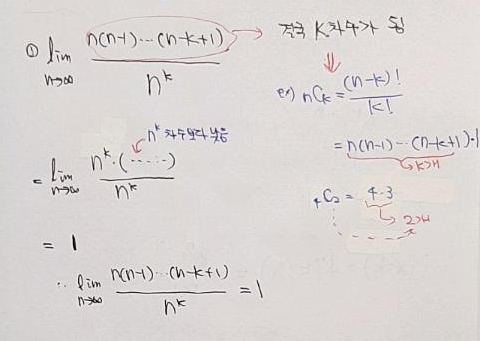
②번식 풀이 (해당 식을 풀이하기 위해서는 자연상수에 대한 개념을 이해할 필요가 있어서 자연상수 내용을 다루었습니다. (하...정말 글씨가....))

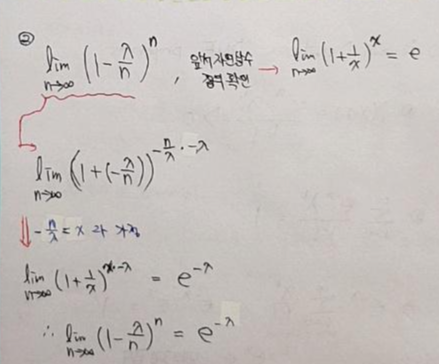
③번식 풀이

최종풀이

• 결국 위와 같은 식을 통해, 특정 시행횟수에 사건이 발생할 수 있는 평균 횟수 "\(\lambda\)"의 정보만을 갖고 random variable(=k)에 속한 확률 값을 알아낼 수 있고, 이를 위해 포아송 확률 함수라 합니다 (포아송 확률 함수를 적용하려고 할 때에는 n이 엄청 커야 한다는 전제를 항상 염두해두시면 좋을 것 같습니다).
• 람다가 고정값이기 때문에 시행횟수와 사건이 발생할 확률이 암묵적(implicit)으로 고정값으로 정해져 있습니다.

• 포아송 확률함수의 총합이 1임을 증명해보겠습니다.

7-1. 포아송분포의 평균식 증명

7-2. 포아송분포의 분산식 증명

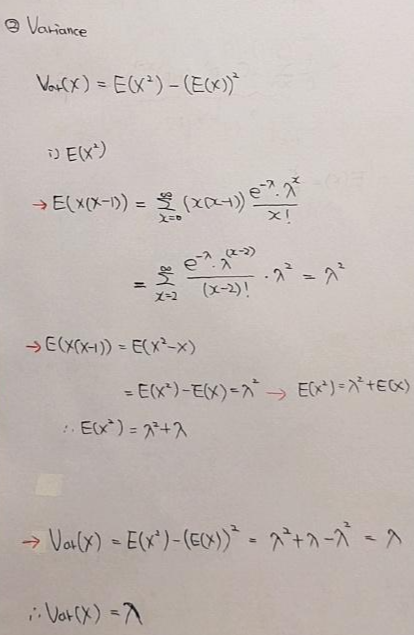
지금까지 이산확률분포의 여러 종류들과, 해당 확률분포의 평균 및 분산식에 대해서 알아보았습니다. 다음 글에서는 연속확률변수 및 연속확률분포에 대한 기본적인 개념들에 대해서 알아보도록 하겠습니다. 

안녕하세요.

이번 장에서는 이산확률분포를 설명하기 위한 여러 개념들에 대해서 살펴보도록 하겠습니다.

1. 확률분포를 사용하는 이유

• 우리는 사회현상, 자연현상을 분석하기 위해 통계적 개념을 이용합니다.
• 예를 들어, 정규(확률)분포는 '일반적인 사회현상을 통계로 나타낼 때, 대부분 평균 주위에 가장 많이 몰려 있고, 그 수치가 평균보다 높거나 낮은 경우는 점점 줄어들게 되는 현상'을 나타내는데, 이러한 현상을 보여주는 확률 분포로써 '정규(확률)분포'를 사용합니다. (정규(확률)분포에 대해서는 연속확률분포를 다룰때 자세히 설명하도록 하겠습니다.)

• 통계학에서는 다양한 확률분포를 사용합니다. 당연히 다양한 자연현상과 사회현상이 있기 때문에, 이러한 현상들을 대표하는 확률분포도 다양하겠죠.
• 그럼 지금부터 확률분포에 대해서 천천히 알아보도록 하겠습니다.

2. 확률분포(Probability Distribution)

• 실험(시행)을 통해 확률변수(random variable) 값이 정해지면, 그 값들의 빈도수를 기반으로한 확률함수를 통해 각각의 변수에 대한 확률 값이 정해집니다.
• 아래 그림에서는 몸무게에 해당하는 정수 값들 (50,60,70,80)이 random variable이며, 상대도수 값이 확률 값입니다.

• 위의 설명을 좀 더 직관적으로 표현하면 아래와 같습니다.

• 실험 데이터들이 많아지면 확률 변수에 따른 확률 값들의 분포를 짐작할 수 있게 됩니다.
• 이러한 실험을 통해서 얻은 확률분포 자체만으로도 굉장히 유용하게 쓰이지만, 해당 확률분포를의 expectation, variance 등의 개념들을 이용하여 유의미한 통계 작업을 하게 됩니다. (expectation, variance 에 대한 설명은 뒷 부분에서 하도록 하겠습니다)

3. Probability Mass Function (PMF)

• 이전 글("2. 확률분포")에서 확률 함수에 대해서 앞서 설명했기 때문에 확률함수에 대한 설명은 생략하도록 하겠습니다. PMF는 간단히 말해 확률 함수가 취하는 정의역이 이산확률변수(discrete probability variable)일 뿐입니다.
  • Probability Mass Function describes a probability distribution over discrete variables.
• 밀도라고 이름을 붙인 이유는 사실 연속확률분포와 관련된 PDF (Probability Density Function)를 먼저 살펴봐야 하는데, 먼저 여기에서는 간단히 "정의" 정도만 언급하고 자세한 설명은 연속확률분포 파트에서 설명하도록 하겠습니다.
• 연속확률분포에서 사용되는 PDF는 밀도라는 개념을 이용합니다. '밀도'라는 것은 부피당 차지하는 질량의 정도(=질량/부피)를 말합니다. 연속확률분포에서는 면적이 확률 값이 되는데 아래 그림을 보면 면적에 해당하는 공간(부피)에 무수한 선들이 빽빽하게 채워져있는 것 처럼 보이게 됩니다. 

• 이산확률분포에서는 질량에 해당하는 하나의 선 자체가 확률 값이 되기 때문에 해당 질량(확률 값)을 도출하는 확률 함수를 PMF라고 부르게 됩니다. 
• PMF는 어떤 discrete random variable에 대한 probability model이라고 할 수 있습니다.

4. 이산확률분포(Discrete Probability Distribution) with PMF axiom

• 우리는 실험을 통해서 확률변수(random variable)을 얻게 됩니다.
• 보통 확률변수를 변량(variance)라고도 하는데, 예를 들어, 몸무게를 측정하는 실험을 통해 얻은 변량 or 확률변수는 50, 60, 70, 80이 될 수 있습니다.
• 만약, 우리가 100명에 대해서 조사한다고 했을 때, "몸무게 50에 해당하는 사람이 2명, 60에 해당하는 사람이 52명, 70에 해당하는 사람이 30명, 80에 해당하는 사람이 16명"이라고 했을 때, 해당 확률변수(50,60,70,80)의 사람 수는 일종의 (빈)도수(frequency)가 됩니다.
• 이러한 확률변수에 대한 (빈)도수를 표로 정리한 것이 도수분포표입니다.
• 그리고 이러한 도수분포표는 상대도수(=도수/도수총합)를 통해 확률 값으로 변경되는데, 이 때 상대도수를 도출하기 위한 함수를 확률함수(PMF)로 볼 수 있습니다.
• 그리고 이러한 PMF에는 아래 그림에서와 같이 두 가지 공리(axiom①, axiom②)가 존재합니다. 그러므로 다음글에서 소개할 다양한 이산확률분포의 확률함수는 아래 두 가지 공리가 항상 성립해야합니다.
  • 특히, 도수에서 상대도수로 바꿀 때, 각각의 도수를 도수총합(=N)으로 나누는데 이를 normalization(정규화)이라고 합니다.

• 앞서 "실험을 통해 얻은 확률분포에서 expectation, variance 등의 개념들이 출현하게 되는데, 이러한 개념들을 이용하여 유의미한 통계 작업을 하게 됩니다."라고 언급했는데, expectation과 variance가 어떻게 쓰이는지 알아보기 전에, expectation과 variance가 무엇인지 먼저 알아보도록 하겠습니다.

5. Expectation (기댓값)

• 기댓값 E(X)를 보통 평균(mean)이라고 합니다.
• 만약 한 반의 시험점수 '평균'이 70점이라고 한다면, 해당 반의 학생 중 아무나 한명을 골랐을 때 시험점수가 70점일거라고 '기대'하기 때문에, '평균'과 '기대값'이라는 용어를 동일시합니다.

5-1. Linearity of expectations

• 선현성에 대한 개념은 나중에 선형대수라는 과목을 다룰 때 더 자세히 설명하도록 하고, 여기에서는 기댓값과 관련된 성질을 알아보는 차원정도로 정리해보도록 하겠습니다.

• 평균(기댓값)이 통계적으로 의미가 있는 이유는 데이터들의 분포를 대표할 수 도 있기 때문입니다.
• 예를 들어 아래 그림에서는 평균이 (대략) 175정도 된다고 볼 수 있는데, 아래와 같은 정규(확률)분포표를 따른다고 하면 실험을 통해 수집한 데이터들이 175에 몰려있다는 것을 추론할 수 있게 됩니다.
• 즉, 평균(기댓값)이 데이터들의 분포를 대표할 수 있게 됩니다. 

6. 편차(Deviation)와 분산 (Variance)

• 앞서 살펴본 '키'관련 확률분포표에서 평균(기댓값)은 데이터들의 분포를 대표할 수 있다고 설명했습니다.
• 아래와 같은 상황에서 A확률 분포는 평균(기댓값)이 데이터들의 분포를 대표할 수 있다고 말할 수 있겠는데, B확률분포를 상대적으로 봤을 때 평균(기댓값)이 데이터의 분포를 대표한다고까지 할 수 있을지 잘 모르겠습니다. 

• B확률 분포와 같은 경우는 평균과 데이터들의 거리가 매우 멀기 때문에, 평균값이 데이터들의 분포를 대표한다고 자신있게 말하기 어렵습니다.
• 그래서 B와 같은 확률 분포를 대표하기 위해서 '평균'과 '평균으로부터 떨어져 있는 데이터들의 거리정도'를 사용해야 B 확률분포를 상징(represent)할 수 있게 됩니다.
• 이때 '평균과 데이터들의 거리'를 '편차'라고 하는데, 해당 확률분포가 평균과의 '편차'가 얼마나 심한지 알기 위해서는 '편차'의 평균을 구하면 됩니다.
• 그런데 아래 그림에서보면 알 수 있듯이 편차가 분명 존재함에도 불구하고 편차들의 평균값이 0이 나올 수 있습니다. (아래 그림에서 변량(확률변수=random variable)은 몸무게에 해당하고, 몸무게의 평균은 70입니다)
• 사실 아래 예시 뿐만아니라 모든 경우에도 편차(변량-평균)의 평균값은 '0'이라는 걸 알 수 있습니다.

• 결국, 편차의 대푯값을 구하기 위해 편차에 존재하는 음수를 양수로 바꾸자는 idea가 나오게 되었고, 음수를 제곱하여 편차의 대푯값을 구하는 '분산'이라는 개념이 나오게 되었습니다. 
• 모든 편차에 제곱을 해주면 항상 양수가 나오기 때문에 아래와 같이 계산하는 방식을 분산이라고 정의하게 됩니다.

• 분산(variance) 공식은 아래와 같이 정리할 수 있습니다.

• 분산은 아래와 같은 속성을 지닙니다.

• 통계학에서는 평균(기댓값)과 분산을 통해 유의미한 연구를 진행하게 됩니다.

7. 표준편차 (Standard deviation)

• 분산식을 보면 제곱 성질로 인해 값이 커진다는 것을 알 수 있습니다.
• 그렇기 때문에 분산식에 루트 (√) 를 씌워주어 값의 크기를 줄여주는데, 이것을 표준편차라고 합니다.
• 즉, 평균으로부터 데이터들이 얼마나 떨어져 있는지의 정도를 표준적으로 알려준다는 의미를 지닙니다.
• 표준편차를 구할 때 식을 RMS (Root Mean Square)이라고도 부릅니다.

이번 장에서는 이산확률분포에 대한 개념과, 확률분포에서 사용되는 유의미한 개념들(평균, 분산, 표준편차)에 대해서 알아보았습니다. 그럼 다음 글에서부터는 이산확률분포의 여러 종류들에 대해서 알아보도록 하겠습니다.

안녕하세요.

이번 장에서는 확률분포에 대한 개념을 설명보겠습니다.

확률분포에 대한 개념을 설명하기에 앞서, 확률변수에 대해서 설명을 해보도록 하겠습니다.

1. Random Variable

• Ways of assigning numerical results to the outcomes of an experiment = A function from the sample space (Ω) to the real numbers (R).
  • 우리가 사람에 대해서 어떠한(임의의(random)) 실험을 한다고 해보겠습니다.
  • 사람의 키를 측정하는 실험을 할 수 도 있고, 몸무게를 측정하는 실험을 할 수 도 있습니다.
  • 즉, 사람이라는 변수 는 어떤 실험을 하는지에 따라 굉장히 다양한 값 (randomness)을 가질 수 있습니다.
  • 만약, '키 측정 실험'을 하게 되면 특정 실수 값 (키) 을 갖게 됩니다. 예를 들어, 우리가 실험을 통해서 얻은 결과가 "키={150~190}"의 범위를 갖을 수도 있습니다. 
• [요약1] 결국, 임의의(random) 실험에 따라서 다양한 변수(variable: 몸무게 or 키 or etc..) 들을 갖게되기 때문에 키, 몸무게와 같은 것들을 하나의 random variable이라고 부릅니다.
• [요약2] 키와 몸무게라는 random variable 종류에 따라 실수 값(or 범위: 키={150~190}, 몸무게={40~80)) 이 정해지기(mapping되기) 때문에 해당 random variable을 하나의 함수라고 보기도 합니다.

2. Probability Variable

• 앞서 Random variable은 '몸무게', '키'와 같은 하나의 함수라고 했습니다.
• Probability variable은 위와 같은 함수(random variable)을 통해 얻은 실수 값이라고 할 수 있습니다.
• 그런데, 어떻게 실수 값 자체가 또다른 변수(probability variable)가 될 수 있을까요?
• 해당 실수 값에 해당 하는 경우가 얼마나 빈번하게 일어나는지 확률함수(\(P{_X}(X=x)\))을 통해 알아 낼 수 있기 때문에, '실수 값' 자체도 확률 값을 알아내기 위한 변수(variable)가 될 수 있습니다.

• 결국, random variable 함수 = 실수 값 = probability variable 이기 때문에, random variable과 probability variable을 따로 구별하지 않고 동의어로 사용하기도 합니다.

3. 확률변수(Random Variable)의 종류

• 확률변수는 크게 두 가지 종류로 나뉩니다.
• 이번 글에서는 각각의 확률변수에 대한 정의만 설명하고, 다음 글에서 이산확률분포를 설명하면서 더 자세히 다루도록 하겠습니다.

3-1. 이산확률변수 (Discrete Random Variable)

• Random variable X가 어느 특정 구간의 모든 실수 값을 택하지 않고 0, 1, 2, ..  와 같은 이산적인 값만을 택하는 변수입니다.

3-2. 연속확률변수 (Continuous Random Variable)

• Random variable X가 어느 특정 구간의 모든 실수 값을 취하는 연속된 구간의 값을 취하는 변수입니다.

4. 확률분포 (Probability Distribution)

• Probability distribution이란 확률변수(random variable)의 모든 값과 그에 대응하는 확률들이 어떻게 분포하고 있는지를 말합니다.
• 앞서 정의한 확률변수의 종류에 따라 확률분포의 종류도 크게 두 가지 (이산확률분포, 연속확률분포)로 나뉘어 집니다.

다음 글에서 부터는 본격적으로 이산확률분포에 대한 개념과, 다양한 이산확률분포를 다루면서, 어떠한 상황속에서 해당 확률분포들을 사용하는지 알아보도록 하겠습니다!

안녕하세요~

이번 장에서는 확률의 개념과 관련된 전반적인 용어 설명들을 하도록 하겠습니다.

1. 확률의 기원

확률이라는 학문은 도박을 그 기원으로 두고 있는데요. 이에 대한 설명이 담긴 영상을 보도록 하겠습니다.

https://www.youtube.com/watch?v=F8TMnn8SW4c 

2. 확률의 사전적 의미

• 확률의 한자 뜻은 다음과 같습니다.
  • 확실할 "확" + 비율 "율" = 확실함의 비율(정도)
• 다음은 영어에서 정의하는 확률의 뜻을 살펴보도록 하겠습니다.
  • Probability is the measure of the likelihood(=%) that an event in sample space will occur.
• 여러 해석이 가능하겠지만 위의 두 설명을 한 단어로 설명하자면 '가능성의 정도'라고 할 수 있겠네요. 당연히 수학분야에서 사용되기 때문에 '정도'를 수치로 표현할 것이구요.
• 가능성이라는 것이 갖는 특징은 어떤 행위가 비결정적인 결과를 낳을 때 사용 가능한 용어라는 점입니다. 
  • 비결정적 결과: 주사위를 던지는 행위
  • 결정적 결과: 물리법칙 → \(E=mc^2 \)

3. 수학적 확률(가능성) = 라플라스 확률

• 위에서 정의한 사전적 정의를 좀 더 구체적으로 표현하면 아래와 같습니다.
  • 확률실험(시행: trial)을 통해 얻은 모든 실험결과(표본공간: Sample space)들 중에서 특정사건(event)이 일어나는 것에 대한 확신(믿음)의 정도(가능성: probability)를 의미 → 어떤 사건(event)이 일어날 가능성을 수치로 나타낸 것
    • 용어1. 확률실험 (시행: trial): 우연의 요소(비결정적 결과→아래에서 설명)를 포함하는 실험으로써 아래 두 가지를 만족하는 실험
      • 1. 같은 조건에서 반복시행이 가능한 실험
      • 2. 매 실행 결과가 무엇이 될지는 알 수 없으나, 실현 가능한 모든 결과들을 시행전에 알 수 있는 실험
      • 3. ex) 주사위 확률시험
    • 용어2. Sample space=표본공간 (Ω,s)
      • Sample space는 확률실험(trial)에서 실현 가능한 모든 결과를 원소(element)로 갖는 집합(set)이다.
      • ex) 주사위 던지는 실험에서의 표본 공간 Ω = {1,2,3,4,5,6}
    • 용어3. Event (사건) = 어떤 시행의 특정한 결과 (표본 공간의 부분집합을 의미)
      • ex) 주사위를 두 번 던졌을 때, "2,4"가 나왔다면 → E = {2,4}

• 위와 같은 정의하에 A사건이 나타날 확률을 표현하는 수학적 확률의 정의는 아래와 같습니다.
  • A의 수학적 확률 = P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{사건 A의 원소 개수}{표본공간의 원소 개수}\) = \(\frac{사건 A가 나타나는 경우의 수}{전체의 경우의 수}\)

• 고등학교때 확률을 배우기 전에 경우의 수를 왜 배우는지 아시겠죠?  아래 목록들은 중고등학교 교과과정에서 배우는 경우의 수 인데,여기에서는 몇몇 부분만 뒷 부분에서 다루도록 하겠습니다.
  • 합의법칙과 곱의법칙
  • 순열, 원순열, 같은 것을 포함하는 순열, 최단 경로의 수, 중복순열
  • 조합, 도형의 개수, 중복조합
  • 분할, 색칠문제, 좌석배치, 숫자 만들기, 이항정리, 이항계수의 성질

4. 확률의 기본 두 가지 이론 

• 확률의 근간을 이루는 이론 중에 가장 기본이 되는 두 가지 확률이론 있습니다.
  • 두 사건의 합집합 (A라는 사건이 일어나거나, B사건이 일어날 경우) 에 대한 확률→ 확률의 덧셈정리
  • 두 사건의 교집합 (A, B 사건이 동시에 일어날 경우 OR A 사건이 일어나고, 연속해서 B 사건이 일어날 경우) 에 대한 확률 → 확률의 곱셈정리  
• 지금부터 이 두 가지 이론에 대해서 알아보도록 하겠습니다.

4-1. 덧셈정리(Addition theorem of probability) with 배반사건(Exclusive evnet)

• A라는 사건이 일어나거나(OR) B라는 사건이 일어날 경우의 확률을 구할 때
• \(\frac{n(A\cup B)}{n(S)}\) = \(\frac{n(A)}{n(S)}\) + \(\frac{n(B)}{n(S)}\) - \(\frac{n(A\cap B)}{n(S)}\)
• \(P(A\cup B) = P(A) + P(B) - P(A\cap B)\)
• 덧셈정리과 관련해서 알아두어야 할 한 가지 개념이 있습니다.
  • 배반사건(Exclusive Event)
    • 우리가 A라는 사건이 일어나거나 B라는 사건이 일어날 확률을 구한다고 했을 때, A라는 사건과 B라는 사건이 동시에 일어나지 않을 수도 있습니다. 이름 그대로 두 사건이 접점이 없이 서로 배타적임을 의미합니다.  그리고, 이러한 개념을 수학적으로 표현하면 다음과 같습니다. → \(P(A\cap B) = 0\)
    • ex) 주사위를 던졌을 때 홀수가 나오거나 (=A사건), 짝수가 나올(=B사건) 경우 A, B 사건을 배반 사건이라 할 수 있습니다.
    • 그래서 A와 B가 서로 배반사건인 상황에서의 덧셈정리는 다음과 같이 정리할 수 있습니다.
      • \(P(A\cup B) = P(A) + P(B)\)  

4-2. 곱셈정리(Multiply theorem of probability) with 종속사건(Dependent event), 독립사건(Independent event), 조건부확률(Conditional probability)

• 확률엥서 곱셈을 하는 경우는 A와 B사건이 동시에 일어날 경우입니다. 
• 또한, 확률 곱셈은 A라는 사건이 일어나고 연속적(순차적)으로 B라는 사건이 일어날 확률을 구할 때도 사용합니다.
• 예를 들어, 아래 그림과 같이 서울에서 대전으로 갈 때 1, 2, 3 맛집이 있고, 대전에서 부산으로 갈때 4, 5라는 맛집이 있다고 하겠습니다. 아침은 A 맛집에서 먹고 점심은 D 맛집에서 먹을 수 있는 확률은 어떻게 될까요?

• 확률의 곱셈정리와 관련해서 알아야할 개념이 있습니다.
  • 위에서 설명한 곱셈정리는 독립사건을 가정하고 있습니다. 그렇다면 독립사건은 무엇일까요?
  • 독립사건을 알아보기 전에 종속사건을 먼저 살펴보겠습니다, 종속사건을 설명하려면 조건부 확률을 알고 있어야 하니 "조건부확률 → 종속사건 → 독립사건" 순서로 글을 정리해보도록 하겠습니다.

4-2-1. 곱셈정리(Multiply theorem of probability) with 종속사건(Dependent event), 독립사건(Independent event), 조건부확률(Conditional probability)

• 확률 곱셈을 이용하여 독립사건, 종속사건, 조건부확률을 알아보도록 하겠습니다 
  
  • 용어1. 조건부확률: B라는 사건이 주어졌을 때 A사건이 일어날 확률
    • Probability of A, Given that B occured
    • P(B|A)
    • 아래 영상에서 조건부 확률과 관련된 재미난 영상을 한 번 확인해보셔도 좋을 것 같습니다.

https://www.youtube.com/watch?v=5DSYQx0iL7I

• • 용어2. 종속사건: A라는 사건이 B라는 사건에 영향을 줄 때 → 즉, 두 사건이 일어나는 순서에 따라 서로 영향을 주고 받을 때, A와 B는 종속사건이라고 합니다.
    • 예를 들어, 52장의 카드를 첫 번째 뽑은 (A사건) 결과가, 두 번째 뽑을 경우의 (B사건) 에 영향을 미치는 경우 → ex) A사건의 표본공간 = 52, B사건의 표본공간 = 51
     Q. 52장의 카드를 순차적으로 뽑는다고 했을 때 모두 검은색이 뽑힐 확률은?

• 용어3. 독립사건: A라는 사건이 B라는 사건에 영향을 주지 않을 때 → 즉 두 사건이 서로 관계가 없이 독립적일 때  
  • 예를 들어, 첫 번째 주사위를 던졌을 때 앞면이 나왔다고 했을 때 (A사건), 두 번째 주사위를 던졌을 때 앞면이 나올 결과에 (B사건) 어떠한 영향도 미치지 않음

5. 독립시행 확률 (베르누이 확률, Binomial Probability) with 순열(Permutation), 조합(Combination)

• 앞서 독립사건에 대해서 알아보았습니다.
• 그렇다면, 독립사건인 상황(조건)에서 사용할 수 있는 확률 개념인 '독립시행 확률'에 대해서 알아보도록 하겠습니다. 
• 우선, 독립시행 확률을 이해하기 위해 순열, 조합에 대한 개념부터 알아보겠습니다.

5-1. 순열

• 순서를 고려하여 나열한 경우의 수 (= 줄 세우는 방법의 수 = 자리 바꿈하는 방법의 수)
  • n명에서 r명을 뽑아 줄 세우는 방법의 수 = \(_{n}P_{r}\) = \(\frac{n!}{(n-r)!}\)
  • ex) "철수, 영희, 민정, 현진, 정태"가 A, B, C 에 앉을 수 있는 경우의 수는?순열

5-2. 조합 (Combination)

• 순서에 상관없이 구성원을 뽑기만 하는 경우
• n명에서 r명을 뽑는 경우의 수 = \(_{n}C_{r}\) = \(\frac{n!}{(n-r)!r!}\) = \(_{n}C_{n-r}\)
• 순열을 또 다른 관점에서 보면 크게 두 가지 action으로 분류할 수 있습니다
  • \(_{5}P_{3}\) → 5명 중 3명을 선택하는 경우의 수 × 뽑힌 3명을 일렬로 나열 하는 수 = \(_{5}C_{3}\)×3!
  • 이러한 관점으로부터 조합 공식을 유도할 수 도 있음

5-3. 독립시행 확률(베르누이 확률, Binomial probability)

• 우리 인생에서 알고 싶은 확률들이 보통은 성공 또는 실패할 확률입니다.
• 이러한 조건에서 공(나온)에 대한 확률이 고정되어 있다고 가정해보겠습니다. 
• 이때 고정된 성공 또는 실패의 확률을 갖고 있는 독립인 사건을 여러 번 시행했을 때 얻은 확률을 독립시행 확률이라 합니다.
• \(_{시행횟수}C_{성공횟수}\)×\(성공확률^{성공횟수}\)×\(실패확률^{실패횟수}\)
• 시행횟수=n, 성공횟수=r, 실패횟수=k, 성공확률=p, 실패확률=p-1 이라고 했을 때
• \(_{n}C_{r}\)×\(p^{r}\)×\((p-1)^{k}\)

6. 전체 확률의 법칙 = 전확률 정리 (Law of Total Probability)

• 전확률 정리는 조건부 확률 (Conditional probability) 로부터 조건이 붙지 않는 확률 (Unconditional probability) 을 계산 할 때 쓸 수 있습니다.
• When we face a complicated problem, sometimes, it gives us simple solution that the complicated problem is broken up simpler pieces. → 베이즈 정리에서 전확률 정리를 이용함 (바로 뒷 부분에서 베이즈 정리 설명)

7. 베이즈 정리

• 우리가 현재 어떤 사건 A에 대학 사전 확률(prior knowledge)을 알고 있다고 하겠습니다.
• 사전 확률은 말그대로 지금까지의 경험을 바탕으로 설정된 A사건에 대한 확률 값입니다.
• 즉, 앞으로의 경험(데이터)에 따라 A사건에 대한 확률 값은 변경(updating)될 수 있습니다.
• 즉, 우리는 이전에 갖고 있었던 사건A에 대한 우리의 믿음의 정도 (사전확률)를 새로 경험하여 얻는 정보(data)에 따라 updating을 해야, 사건A에 대한 확률 값이 점점 신뢰성을 갖게 될 것입니다.
• 정리하자면, 새로운 정보를 얻었을 때 베이즈 정리를 이용해 해당 사건에 대한 최신 확률 값을 얻을 수 있습니다.
• 예시
  • H라는 사건이 일어날 확률 = P(H) 
  • H라는 사건이 참이라는 조건하에 D가 일어날 수 있는 확률 = P(D|H)
  • D라는 데이터가 주어졌을 때 H가 일어날 확률 = P(H|D) = \(\frac{P(H\cap D)}{P(D)}\) = \(\frac{P(H)P(D|H)}{P(D)}\)
  • 분모가 되는 P(D) 부분을 전확률 정리로 풀어 쓸 수 있다 → 자세한 것은 문제를 통해 설명

8. 통계적 확률

• 주사위를 한 번 던졌을 때 1이 나올 확률이 6이라고 알고 있습니다. 다시말해, 주사위를 6번 던져야 1이 한 번 나올 것이라는 말과 같다고 할 수 있습니다.
• 하지만 현실에서는 주사위를 6번 던져도 1이 나올 확률이 1/6이 안될 수 도 있습니다.
• 여기에서는 주사위를 6번 던졌으니 시행횟수가 6입니다. 그런데, 이 시행횟수를 한 없이 늘리다보면 결국 1이 나올 확률이 우리가 알고 있는 수학적 확률인 1/6에 근사하게 됩니다.
• 즉, 어떤 시행(trial)을 여러 번 반복했을 때 \(\frac{나온횟수}{시행횟수}\) 는 시행횟수가 한 없이 커짐에 따라 특정한 값에 가까워지는데, 이를 통계적 확률이라 합니다. ex) 타율
• 실제로는 시행 횟수를 한 없이 커지게 할 수 없으므로 시행횟수가 충분히 클 때의 값을 통계적 확률로 봅니다.
• 결과적으로, 시행횟수가 커지다보면 결국 통계적 확률이 수학적 확률에 가까워진다는 철학이 깔려있습니다.

지금까지 확률에 대한 개념과 관련된 전반적인 개념을 다루었습니다. 다음 장에서는 확률분포라는 개념을 이해해보도록 하겠습니다.

[정리]

1. 확률은 "확률실험(시행: trial)을 통해 얻은 모든 실험결과(표본공간: Sample space)들 중에서 특정사건(event)이 일어나는 것에 대한 확신(믿음)의 정도(가능성: probability)를 의미" → 어떤 사건(event)이 일어날 가능성을 수치로 나타낸 것

• A의 수학적 확률 = P(A) = \(\frac{n(A)}{n(S)}\) = \(\frac{사건 A의 원소 개수}{표본공간의 원소 개수}\) = \(\frac{사건 A가 나타나는 경우의 수}{전체의 경우의 수}\)

2. 확률에는 두 가지 기초연산이 있다.

2-1. 덧셈정리(Addition theorem of probability) with 배반사건(Exclusive event)

• 확률에서 덧셈이 사용되는 경우: A라는 사건이 일어나거나(OR) B라는 사건이 일어날 경우의 확률을 구할 때
• \(\frac{n(A\cup B)}{n(S)}\) = \(\frac{n(A)}{n(S)}\) + \(\frac{n(B)}{n(S)}\) - \(\frac{n(A\cap B)}{n(S)}\)
• \(P(A\cup B) = P(A) + P(B) - P(A\cap B)\)
• 배반사건(Exclusive Event) = \(P(A\cap B) = 0\)

2-2. 곱셈정리((Multiply theorem of probability) with 종속사건(Dependent event), 독립사건(Independent event), 조건부확률(Conditional probability))

• 확률에서 곱셈이 적용되는 경우: A라는 사건이 일어나고 연속적(순차적)으로 B라는 사건이 일어날 확률을 구할 때 사용한다.
• 어떤 사건이 연속적으로 일어날 때 이전 사건이 다음 사건에 영향을 미치는 경우에 필요한 개념 및 수식
  • 종속사건(Dependent event) 
  • \(P(A\cap B)\) = P(B|A)P(A) = P(A|B)P(B)
  • 조건부 확률 (Conditional Probability): P(B|A) -> A라는 사건이 발생했을 때 B라는 사건이 발생할 확률
• 어떤 사건이 연속적으로 일어날 때 이전 사건이 다음 사건에 영향을 미치지 않는 경우에 필요한 개념 및 수식
  • \(P(A\cap B)\) = P(A)P(B)
  • 독립사건(Independent event) → P(B|A) = P(B)

3. 독립시행 확률 (베르누이 확률, Binomial probability)

• 고정된 성공 또는 실패의 확률을 갖고 있는 독립인 사건을 여러 번 시행했을 때 얻은 확률을 독립시행 확률이라 한다.
• 시행횟수=n, 성공횟수=r, 실패횟수=k, 성공확률=p, 실패확률=p-1 이라고 했을 때
• \(_{n}C_{r}\)×\(p^{r}\)×\((p-1)^{k}\)

4. 베이즈 정리 with 전확률 정리

• 이전에 갖고 있었던 사건A에 대한 우리의 믿음의 정도 (사전확률)를 새로 경험하여 얻는 정보(data)에 따라 updating할 수 있다.
• 즉, 새로운 정보를 통해 얻은 한 사건A에 대한 최신 확률 값을 베이즈 정리를 통해 얻을 수 있다.
• D라는 데이터가 주어졌을 때 H가 일어날 확률 = P(H|D) = \(\frac{P(H\cap D)}{P(D)}\) = \(\frac{P(H)P(D|H)}{P(D)}\)

안녕하세요.

이번에 확률과 통계에 대해서 글을 작성하려고 합니다.

제가 확률,통계를 블로그로 정리해야 겠다고 생각한 이유는 아래와 같이 몇 가지로 정리할 수 있을 것 같아요.

1. "AI, 데이터 사이언스, 머신러닝, 딥러닝"의 뿌리이기 때문

보통 AI, 데이터 사이언스, 머신러닝, 딥러닝을 응용수학이라고들 하는데

아마 여러 수학적 지식들이 복합적으로 적용되서 그런게 아닐까 싶어요.

예를 들어, 딥러닝의 어떤 모델 한 가지만 하더라도 선형대수, 통계학, 미적분학, 최적화 등등 정말 다양한 수학적 측면에서 해석할 수 있다는 뜻이죠.

2. 인간의 (철학적) 주장을 과학적으로 포장하기 위한 유일한 도구이기 때문

만약 제가 "비트코인이 주식보다 좋아?"라고 말했다고 해볼게요.

A라는 사람은 "비트코인이 더 좋아. 왜냐하면 비트코인은 수익성이 최대 130%까지 가능하거든"

이 말을 듣고 B라는 사람에게 비트코인을 하자고 했더니

B라는 사람이 "무슨소리야. 주식이 더 좋아. 주식 수익성이 최대 20%까지 이긴 해도 비트코인 처럼 단 시간에 원금 다 날리는 경우는 없거든"

이렇게 말했다고 해볼게요.

누구의 말을 믿어야 할까요? 

사실 누구의 말을 믿든 결국 자신의 철학에 따라 선택할 수 밖에 없을거에요.

만약 안정성에 더 우선순위를 두어야 하는 상황이라면 주식을,

주식의 최대 수익성이 아무의미 없는 경우는 비트코인에 투자하는게 더 좋을 거에요.

(빨간색: 주식/ 파란색: 비트코인 -> 100 원금 투자했을 때 우측으로는 이익, 좌측으로는 손실)

(아직 통계의 개념이 명확하지 않으신 분은 아래 그림을 굳이 이해하지 않으셔도 됩니다. 차차 설명해드릴게요!)

좀 더 설명해보자면...

보통 과거에는 많은 사람들이 안정성에 가치를 많이 두었기 때문에 주식을 많이 선택했을거에요. 

아무도 모르는 사람들이 주식을 해도 최소 -35%~25% 사이의 수익성이 보장됐기 때문에 원금을 날릴 경우가 없었기 때문이에요.

그런데 내가 아무리 25%의 수익성을 낸다고 해도 집값을 사는데 50년이 걸린다고 하면 이게 의미가 있을까요?

이러한 경우에는 손실을 감안하고 비트코인에 올인하려고 하는경우가 있을거에요. 

정치든, 과학이든, 마케팅이든 항상 자신의 아이디어(또는 주장)가 더 좋다는 것을 증명하거나

실제 사례를 보다보면 자신의 아이디어가 좋을 때도 있고 아닐 때도 있어요.

(또는 자신이 주장하는 인과관계가 타당하다고 인정을 받아야하는 경우도 있는데, 이러한 인과관계가 항상 성립하는 경우는 드물겠죠)

예를 들어, 화이자 백신이 좋다고는 하지만 어떤 사람들은 접종하면 사망하는 경우도 있습니다. 그렇다면 화이자 백신이 좋다고 할 수 있을까요?

여기서부터 화이자 사장은 통계 개념을 통해 다음과 같은 주장을 합니다.

"화이자를 맞았을 때 평균적으로 코로나에 걸릴 확률이 적습니다. 또한 다른 회사의 백신과 비교했을 때 코로나에 걸릴 확률이 적습니다. 그러므로 화이자 백신은 다른 백신들보다 더 좋다고 할 수 있습니다" 

결국 통계학이라는 도구를 통해서 무언가가 더 좋다 나쁘다고 하는 것은 절대적인 사실이 아니라

상대적인 관점에서 비교분석하여 얻어낸 결과라고 할 수 있습니다.

3. 확률을 품은 통계

결국 통계라는건 어떤 현상을 설명하기 위해 확률을 받아들인 학문이라고 보면 될 것 같아요.

그래서 제 개인적으로 통계학이라는 학문을 아래와 같이 받아들이고 있습니다.

"통계학은 인류를 위한 진실(확실성:certainty)을 만들기 위해 불확실성(uncertainty; 확률)과 타협한 학문"

다시말해 통계학은 확률(불확실성)을 기반으로 하여 어떠한 현상(집단)을 설명(대표)하기 위한 도구이며,

해당 현상(집단)들을 서로 비교 분석하여 자신들의 주장이 합리적임을 증명하기 위해 사용하는 도구라고 이해하고 있어요!

4. 국가를 통치하기 위해 만들어진 학문이 곳 통계학

https://www.youtube.com/watch?v=YlGMHmzeW3Y 

간단하게 이 글을 쓰기로한 동기에 대해서 작성해보았습니다.

그럼 본격적으로 다음 글에서 확률부터 천천히 글을 작성해 보도록 하겠습니다~

안녕하세요~

정말 오랜만에 글을 쓰네요 ㅎㅎ

제 블로그 조회기록을 보니

GPU관련 조회수가 많아지는 것 같더라구요!

그래서 이번 글에서 

지난 내용들을 영상으로 요약정리해봤어요~

CUDA study를 하면서 

제가 발표했던 영상이니 많이 봐주세요~! ㅎㅎ

(발표는 1:30초 부터에요!)

안녕하세요~

이번에는 관악구에 위치한 샤로수길 음식점들을 

소개하려고 합니다~

해당 페이지를 샤로수길을 방문할 때마다

업데이트가 될 것 같아요! ㅎㅎ

1) 2020.10.23(금) 방문

이 날 방문했던 샤로수길 음식점은 

와썹맨 영상을 보고 갔습니다 ㅎㅎ

[식사 편]

1. 텐동요츠야

저는 점심시간인 11:50즘에 도착했어요.

10분 정도? 웨이팅 하고 나서 식사를 할 수 있었는데,

12:00에 줄을 보니까 조금만 늦었어도 30분 이상은

웨이팅 할 뻔 했어요..ㅎ

첫 방문이라 스페샬텐동을 주문했습니다~ 

주방이 오픈이라 음식 만드는 걸

보는 재미도 있었어요~

주문한 스폐샬텐동과 미소국~

저는 개인적으로 튀김이 얇은걸 

선호해서 좋았어요~

2. 킷사서울

킷사(喫茶)는 먹을 '끽', 차 '차', 라는 한자어를 모아 차를 마시다라는 뜻이라고 해요.

(경양식 집인데 왜 이름을 그렇게 지었는지 나중에 가서 물어봐야겠다;; ㅎㅎ)

영업시간 --> 11:30 ~ 22:00

휴식시간(break time) --> 15:00 ~ 17:00

들어가자마자 일본 경양식집 분위기가 났어요.

희한하게도 창가에 햇살이 들어오는데

내부 공간이 따뜻해보이네요 ~

이 곳의 대표음식인 

단뽀뽀 오므라이스와 쇼유에비동을 주문했어요~

주방은 오픈 되어 있었고

음식을 만드는 모습을 볼 수 있었어요 ~

(오픈되어 있으니 신뢰감이 ㅎㅎ)

짜잔~

단뽀뽀 오므라이스~

쇼유에비동 ~~

쇼유는 일본식 간장이라고 보시면 되고,

에비(えび)`는 새우, `동(どん)`은 덮밥이라는 뜻이라고 합니다~

대체적으로 맛도 괜찮았어요~

혹시 가로수길에서 격식을 갖추어야 할 

중요한 약속이 있으면

이곳에서 식사 대접하는 것도 

좋을 것 같다는 생각을 했어요~ ㅎㅎ

3. 지구당

샤로수길 규동 맛집인 

지구당이에요~

지구당 영업시간은 17:00 ~ 21:00 이고, 

마지막 주문은 영업 종료 30분 전인 

20:30분이에요~

일단 먼저 도착하시면

벨부터 눌러주시고, 인원수를 말씀해주세요~

벨을 누르시면

주인분께서 여기 창문으로 빼꼼 나오셔서

안내를 해주신답니다~

우선 들어와서 시그니처 메뉴인

규동을 주문했어요~

주문을 기다리는 동안 

규동 맛있게 먹는 법도 알아봤답니다 ㅎㅎ

이전에 판매했던 오야꼬동은

더 이상 판매하지 않고 있으니 

참고해주세요!

주방이 오픈되어 있고,

음식을 만드는걸 가까이서 볼 수 있어서

신뢰가 가요~!

식당 규모가 매우 작기 때문에 

(거의 7~8명만 들어올 수 있을 정도?)

테이블은 없고, 

아래와 같은 곳에서 식사를 할 수 있었어요~!

드디어 주문을 한 규동이 나왔어요~!

반숙계란도 같이~!

아까 맛있게 먹는 법을 

봤으니 그대로.... ㅎㅎㅎ

지구당은 식사를 할때 과하게 

떠들면 주인분께서 정중히 

말씀해주세요 ㅎ

그래서 샤로수길에서 혼자 조용히 식사

하고 싶으실 때 여기를 방문해주시면 더 좋을 것 같습니다~!

[후식 편]

1. 라미스콘

저도 와썹맨을 보고 알았는데

라미스콘이 건강한 빵을 만들려고

굉장히 노력을 하는것 같더라구요!

(참고로 라미스콘은 종로 익선동에도 있어요!)

라미스콘 링크

저도 빵을 좋아하긴 하지만 밀가루 때문에

피하긴 했는데 

보기도 좋은 빵이

먹기도 좋더라구요 ㅎㅎ

종류가 굉장히 다양하죠!?

저희는 와썹맨에 나왔던

치즈 수플레와 생크림,

아인슈페너 카페 모카, 라미 밀크 티를

주문했어요~

짜잔~ 

보통 치즈 케익은 느끼해서 잘 못 먹는데

이 케익은 느끼한 건 잘 못 느꼈고

우유맛이 더 잘 느껴져서 거부감 없이 먹었던 것 같아요 ㅎㅎ

Updating.... ㅎㅎ

안녕하세요~

이번에는 구리시에 위치한 

모던기와라는 한옥카페를 

소개하려고 합니다~

경기도 구리시 아차산로 37

구리역에서 차로

대략 20분이 소요가 되네요!

모던기와에 도착해서 주차를 하고 

안쪽으로 계속 들어가다 보면..

계단이 나옵니다!

계단을 올라가시면...

짜잔~

모던기와 카페가 나와요 ㅎㅎ

주문은 안쪽으로 들어가셔서 해야해요!

카페 내부에요

이 곳에서 주문을 하시면 됩니다!

진동벨을 갖고 밖에서 기다리다가

진동벨이 울리면 주문한 메뉴를

가지고 오시면 됩니다!

밖에도 테이블이 있어서

저희는 밖에서 커피를 마셨어요 ㅎㅎ

이때가 주말 저녁즘이여서 

카페에 오신 분들이 많더라구요

원래 한강을 보면서 먹을 수 있는 자리가 있어

그곳에서 사진을 찍었어야 했는데...

다음엔 평일에 방문해서 재업로드 해야겠어요! ㅎㅎ

안녕하세요~

이번에는 남양주시 평내동에 위치한

전라도 향토음식

김삿갓 밥집을 

소개하려고 합니다~

전라도 향토음식 하면 어마어마한 몇첩 밥상이 생각나시죠?ㅎ

그럼 한 번 전라도 향토음식을 맛보러 출발해보겠습니다!

경기 남양주시 경춘로 1158

(매주 월요일은 휴무에요!!!!!!!!!!!!!!!!!!!!!!!)

구리역에서 김삿갓밥집까지는 

20분 정도가 소요됩니다!

영업 날짜 및 시간이 나와있으니

참고하세요!

(월요일은 휴무에요~~)

저날 평일 11:45(AM)분즘에 도착했는데

30분 정도 웨이팅 했던 것 같아요 ㅜㅜ

주말이나 12시에 도착하면

최소 1시간 이상 웨이팅은 기본인거 같았어요 ㅜㅜ

그래서 아래와 같이 안내문이 있었습니다~

(다른 음식점에는 카톡으로 대기 번호 받기도 하는데

여기는 그런거 없이 계속 줄서있어야 됐어요 ㅜㅜ)

그리고 1인 식사는 불가능 하다는 점ㅜㅜ!

웨이팅이 거의 끝나갈 무렵

입구 쪽에서 대기 하고 있는데

김삿갓밥집에 대한 여러 설명들을

글로 친절하게 써놓으셨어요!

드디어 들어가기 직전!

입구 좌측에 화장실이 있어요!

드디어 입성!

저희는 안쪽으로 안내 받았습니다~ ㅎ

저희는 삿갓정식을 시켰어요~~

친절한 설명까지~

드디어 음식이 도착! 두둥!!

와.... 14000원 치고는 푸짐하죠!

(예전에 코엑스에서 곰탕 하나가 14000원이었던 것 같은데;;;;;;;;;;;ㅎㅎ)

각종 나물반찬에 ~

수육~~

조기~~

보리밥에 호박죽~~~

이 집의 시그니처인 들기름까지~~~

아 정말.. 다 먹고 그날 움직이질 못했던 것 같아요..

웨이팅이 길어서 힘들었지만

그만큼 훌륭한 가성비로

먹을 수 있어 좋았습니다!!!

한 번쯤은(?) 꼭 방문하셔서 

푸짐하게 식사하셔도 좋을 것 같아요! ㅎㅎ

안녕하세요 이번글에서는 CNN 모델을 평가하는 또 다른 지표인 F1 score에 대해서 알아보도록 할거에요.

앞서 "5.CNN 성능은 어떻게 평가하게 되나요?"라는 글에서 봤듯이 CNN은 accuracy 기반을 하여 CNN 성능을 평가한다고 말씀드렸어요.

하지만 어떠한 상황에서는 accuracy를 기반으로 하는 것 보다는 다른 성능지표를 사용하는것이 더 좋을 수 있어요. 그래서 이번글에서는 accuracy를 사용하면 좋지 않은 상황과 이런 상황에서 대안이되는 성과지표(measurement)를 알아보도록 할게요.

이번 글의 이미지와 모든 내용은 아래 유튜브 영상에서 참고하였으니 아래영상을 보시는걸 추천드립니다.

<1.Confusion Matrix>

로봇에게 A라는 글을 보여주고(input) 로봇이 A라고 답(answers)했을 때 아래 테이블 처럼 1이라는 표시를 해줍니다. 만약 B라는 글을 보여줬는데 D라고 답한다면 (B,D) 구역에 1이라고 표시를 해볼게요.

이러한 과정을 반복해서 최종적으로 아래와 같은 테이블을 얻었다고 해봅시다. 로봇A, 로봇B는 각기 다른 결과들을 보여주었어요 (아래와 같은 결과(Matrix)를 Confusion Matrix라고 합니다). 그렇다면 우리는 두 로봇의 Confusion Matrix를 봤을때 어떤 로봇모델을 쓰는것이 좋을까요? 

위에서 질문한 답을 하기 위해서 "Accuracy, Recall, Precision, F1 score"라는 성능평가 지표를 보고 어떤 로봇(모델)을 사용할지 결정하게 되는데, 이러한 개념을 이해하기 위해서는 먼저 TP, TN, FP, FN이라는 개념에 대해서 알아봐야해요. 

<2. TP(True Positive), TN(True Negative), FP(False Positive), FN(False Negative)>

특정 클래스를 잘 구분하는지 알아본다고 해볼게요.

만약 A라는 클래스를 잘 구분하는지 알아본다고 했을 때, 아래 두 가지 개념이 유용하게 사용돼요

Positive and Negative: 정답과 관계없이 A 클래스 입장에서 모델이 A라고 분류하면(+) A기준에서는 Positive하게 분류한것이고, A라고 분류하지 않으면(-) Negative 하게 분류한거에요.

True and False: 정답과 관련하여, 예측과 정답이 일치하면 True, 예측과 정답이 일치하지 않으면 False로 분류해요.

1-1) TP (True Positive)

로봇이 A 클래스를 얼마나 잘 분류하는지 알아본다고 해볼게요 (A관점에서 positive, negative를 나눈다고 가정하겠습니다.)

예를들어, A클래스를 보여주고 A라고 (positive) 올바르게 (True) 예측하면 A에 대해서 True Positive하다고 할 수 있어요 (True Positive for A).

1-2) FP (False Positive for A)

로봇이 A 클래스를 얼마나 잘 분류하는지 알아본다고 해볼게요 (A관점에서 positive, negative를 나눈다고 가정하겠습니다.)

예를들어, B,C,D 클래스를 보여줬을 때 A라고 (positive) 잘 못 판단(False) 한다면 A에 대해서 False Positive하다고 할 수 있어요 (False Positive for A).

1-3) FN (False Negative for A)

로봇이 A 클래스를 얼마나 잘 분류하는지 알아본다고 해볼게요 (A관점에서 positive, negative를 나눈다고 가정하겠습니다.)

예를들어, A 클래스를 보여줬을 때, A가 아니(Negative)라고 잘 못 (False) 판단하는 경우를 A에 대해서 False Negative 하다고 해요 (False Negative for A).

1-4) TN (True Negative for A)

로봇이 A 클래스를 얼마나 잘 분류하는지 알아본다고 해볼게요 (A관점에서 positive, negative를 나눈다고 가정하겠습니다.)

예를들어, B,C,D 클래스를 보여줬을 때, A가 아니(Negative)라고 올바르게 판단(True) 하는 경우를 A에 대해서 True Negative 하다고 합니다 (True Negative for A).

<사진5>

<3. Accuracy>

위에서 언급한 개념들을 토대로 우리가 사용할 수 있는 첫 번째 성능지표는 Accuracy에요. Accuracy는 아래와 같은 수식을 통해 계산이되요

(아래영상은 TP로만 계산이 되었네요. 개념만 이해하시면 될 것 같습니다.)

이런 경우에는 Accuracy 지표를 이용하여 Model1, Model2를 평가하고 Model1을 사용하게되면 실제로 어떤 class(A,B,C,D)를 보여줘도 Model2보다 높은 확률로 정답을 도출해낼거에요.

하지만, 위와 같은 경우는 Model1, Model2 모두 실제 테스트 클래스(actual values)가 A=10, B=10, C=10, D=10 으로 각각 동일할 거에요. 이럴때 머신러닝이 학습하기 위한 데이터셋의 class가 balance하게 구성되어 있다고 이야기해요. 그렇다면 class가 imbalance한 구조에서도 accuracy라는 지표가 효율적일까요?

예를들어, 의학 이미지 데이터들을 보면 정상인(normal)에 해당하는 데이터셋은 굉장히 많이 있는 반면에, 병(변)이 있는 사람들의 데이터셋은 굉장히 적어요. 만약 정상인의 MRI 이미지가 1000개가 있고, 암환자의 MRI 이미지가 100개가 있는 경우에 accuracy 지표를 쓰면 어떤 문제가 일어날까요?

1) Accuracy 문제점

위에서 언급한 Accuracy measurement는 imbalanced dataset을 갖고 있는 상황에 따라서 그닥 효율적이지 않은 성능지표가 될 수 있어요. 만약 위의 예시처럼 모든 클래스의 데이터가 10개씩 balance하게 있지 않고 아래와 같이 A클래스에만 집중적으로 데이터가 몰려있다면 어떻게 될까요? A기준에서 봤을때는 아래 성능지표가 좋을 수 있지만, B,C,D 관점에서 보면 해당 모델을 평가하는데 accuracy가 좋은 measurement가 될 수 있을까요?

한 눈에 보더라도 모든 데이터가 A에 쏠려있기 때문에 accuracy가 B,C,D에도 적용이 되기에는 B,C,D에 대한 모집단이 부족한걸 보실 수 있으실 거에요.

아래 예시를 통해 살펴볼게요.

먼저 Model1을 오로지 A관점에서 보면 모델이 그닥 좋지 않을 수 있어요. 왜냐하면 100/(200=100+80+10+10) = 50%의 정확성을 보이기 때문이에요. 하지만, B,C,D 관점에서 보면 모두 80% 이상의 정확성을 보이기 때문에 Model1은 B,C,D 관점에서는 좋은 모델이고, A모델 관점에서는 좋지 않은 모델이되요.

Model2의 경우 A관점에서 보면 198/200 = 99%의 정확성을 보여 좋겠지만, B,C,D의 관점에서 보면 모두 10%의 정확성을 보이기 때문에 Model2가 좋은 모델이라 할 수 없어요.

이런 경우 Accuracy를 적용해 Model을 평가하게 되면 어떻게 될까요? 이런 상황에서는 특정 class의 샘플수와 해당 class의 정확성에 많이 의존해서 accuracy가 도출될 수 밖에 없게되요. 위에 있는 예시를 보더라도, Model1,2에 입력된 A클래스가 앞도적으로 많고, A클래스에 대한 accuracy에 따라서 전체 클래스(A,B,C,D)에 대한 accuracy 가 결정이돼요. 

우리가 의학적인 목적으로 머신러닝을 이용한다고 해볼게요. 1000명이 진료를 보러 왔는데 실제 990명이 정상인이고 나머지 10명이 병(변)이 있다고 해보겠습니다. 이 머신러닝 모델은 정상인들에 대해서는 100%의 정확성을 보였고, 실제 병(변)이 있는 분들에 대해서는 50%의 확률을 보였다고 할게요. 전체적으로 볼때 1000명의 환자중 995명을 제대로 판별했으니 99.5%의 정확성을 보인다고 할 수 있겠죠. 그럼, 이 병원을 신뢰하고 가야하는건가요? 실제로 병(변)이 있는 분들께서 이 병원을 찾았다가는 큰 낭패를 보시게 될 거에요. 

위와같이 데이터셋의 class가 imbalance하게 되어있다면 어떤 성능지표를 사용해야 하는걸까요? 이럴때 상용될 수 있는 기법이 F1 score를 계산하는거에요. 그럼 지금부터 F1 score 개념을 이해하기 위해 Precision, Recall 개념을 차례대로 살펴볼게요.

<4. Precision>

Given a class prediction from the classifier, how likely is it to be correct? 

각각의 클래스에 대해서 정확하게 분류됐는지를 알고 싶을 때, Precision이라는 개념을 사용해요. 아래 예시를 기준으로 A 상황에 대한 Precision을 보고자 한다면, 9/(9+1+5+0=15) 가 되겠네요.

일반화해서 보자면, 머신러닝 모델이 특정 클래스를 prediction할 때, 해당 클래스에 대한 prediction(예측) 얼마나 잘 맞을지를 보여주는 지표라고보시면돼요. 즉, 특정 클래스에 대해 prediction 했다는 것만 고려한다는 것에대한 숨어 있는 의미는 Negative 요소를 고려하지 않는다는 점이에요. 

<TP 예시>

<FP 예시>

Model1의 Average precision 결과를 보면 Accuracy와 비교해서 비교적 class A에 덜 의존적인 결과를 볼 수 있다는 것을 알 수 있어요.

Model2도 마찬가지네요.

결과적으로 보면 Accuracy는 imbalance한 dataset 상황에 있을 때, 특정 class의 accuracy에 지나치게 의존적일 수 있지만, Precision은 평균을 취함으로써 그 의존성을 줄여주게 됩니다. 즉, 다시말해 precision은 머신러닝 모델이 A or B or C or D를 prediction할 때, 평균적으로 얼마나 정확하게 prediction하는지 알려주는 성과지표라고 할 수 있겠어요.

<5. Recall>

Given a class, will the classifier detect it?

어떤 클래스가 주어졌을 때, 주어진 클래스를 다른 클래스들 중에서 잘 검출(detect)하는지 알고싶을 때 사용하는 개념이 recall이라는 개념입니다. 예를들어, 실제 A 클래스가 머신러닝 모델에 들어 왔을 때, 9번 정도 A라고 예측(prediction)했다면, "A,B,C,D 클래스"들 중에서 A 클래스를 90% 잘 검출해냈다고 할 수 있어요.

그래서 아래같와 같이 A에 대한 recall은 9/(9+1+0+0) 이 됩니다.

<TP 예시>

<FN 예시>

Recall 또한 각각의 클래스에 대한 recall의 평균을 취하기 때문에 한 class의 accuracy에 지나치게 의존하지 않게 됩니다.

Recall 또한 마찬가지로 imbalance한 dataset 상황에 있을 때, 각 클래스에 대한 평균을 취함으로써 특정 class의 의존성을 줄여주게 됩니다. 즉, 다시말해 recall은 머신러닝 모델이 특정 class에 대해 (특정 class가 test 입력으로 들어올때), 평균적으로 (전체 (A,B,C,D) 클래스들 중에서 정답이 되는 특정 클래스를) 얼마나 잘 detect(검출)하는지 알려주는 성과지표라고 할 수 있겠어요.

<6. F1-score>

앞선 글에서 봤듯이 클래스가 imbalance한 문제에서는 precision과 recall이 유용하게 사용될 수 있어요. 그렇다면 precision과 recall 지표를 동시에 잘 이용한다면 imbalance dataset이 주어진 상황에서 좀 더 좋은 모델을 선택할 수 있지 않을까요?

다시말해, 특정 class의 accuracy에 덜 의존하면서, precision(Given a class prediction from the classifier, how likely is it to be correct? )과 recall(Given a class, will the classifier detect it?)이 내재하고 있는 두 가지 상황(어떤 관점에서 모델을 판단할지)을 모두 고려하면, 좀 더 객관적이고 다양한 상황을 고려할 수 있는 평가지표가 될거에요.

일반적으로 어떤 두 개념을 동시에 고려할 때 도입되는 개념은 평균입니다. 그래서 Precision과 Recall 두 개념(속에 녹아있는 상황들)을 적절하게 고려해주기(나타내주기) 위해 Precision과 Recall의 평균을 취하게 되는거죠. 

<사진1>

평균을 내는 방식에도 종류가 여러가지인데, 일반적으로 산술평균을 내게 되면 precision과 recall 두 개념(상황)을 모두 고려할 때 문제가 발생할 수 있어요. 앞서 Precision과 Recall에서 얻었던 장점이 특정 클래스의 accuracy에 의존적이지 않다는 점이라면, Precision과 Recall을 개념을 혼합할 때도 조심해야하는 부분이 두 값의 평균(precision과 recall을 혼합했을 때)값이 precision 또는 recall 두 개념을 적절하게 고려할 수 있는 값을 의미하는가에요.

precision = (p(A)+p(B)+p(C)+p(D))/4 = p

recall = (r(A)+r(B)+r(C)+r(D))/4) = r

산술 평균값 = (p+r)/2

예를들어, 어떤 A라는 모델에서 precision 값이 0.9이고, recall 값이 0.1이라고 해볼게요. 이 결과 산술평균값은 0.5일거에요. B라는 다른 모델에서는 precision 값이 0.5이고, recall 값도 0.5라고 해볼게요. 이 결과 산술평균값도 0.5에요. 그런데, A라는 모델에서 얻은 0.5라는 값이 precision, recall을 동시에 잘표현해주나요? precision의 의미를 내포한다고 하기에는 너무 결과값(평균값)이 작은것 같고, recall을 표현하기에는 결과값이 너무 큰 것 같지 않나요? 

우리가 알고 싶은건 precision과 recall 이라는 두 개념을 동시에 잘 아울러서 보여줄 수 있는 결과값이 존재하는가에요. 즉, precision과 recall 값들의 차이가 나지 않아야 precision과 recall 모두 성능이 좋은지 아닌지를 이야기 할 수 있게 되는거에요. precision과 recall 두 값이 차이가 많이난다면 두 개념 중에 특정 값(precision or recall)에 의존적이게 됩니다. 

precision, recall 값이 차이가 많이 난다면 당연히 두 개념이 머신러닝 모델 성능에도 문제가 있다고 보는것이 합리적인 판단이에요. 그래서 precision과 recall 이라는 상황을 고려할 때, 두 상황을 "모두" 적절하게 고려했는지를 판단하려면 precision과 recall 값의 차이가 심하게 나면 안됩니다. 

그래서 precision과 recall 간에 차이가 급격하게 나는 것 보다, precision과 recall을 혼합한 결과가 두 값의 차이가 적을 때 높아야 두 상황(precision, recalll)을 적절하게 고려했다고 할 수 있을거에요. 

이러한 철학을 기반으로 도입된 개념이 '조화평균'이라는 개념이에요.

1) 조화평균(harmonic mean)

말을 그대로 풀어 쓰면, 어떤 두 값에 대한 평균을 낼때 두 값이 조화롭다면(두 값의 차이가 많이 나지 않는다면) 높은 값을, 두 값이 조화롭지 않다면 (두 값의 차이가 많이 난다면) 낮은 값을 도출해준다는 철학을 갖고 있어요.

예를들어, 어떤 모델이 precision = a = 0.9 라고 하고, recall = b = 0.1을 기록했다고 하고, 다른 모델이 precision = a = 0.5, recall = b = 0.5라고 했을 때의 조화평균을 구하면 아래와 같아요.

첫 번째 케이스는 precision과 recall의 차이가 너무 크기 때문에 결과값이 낮게 나왔어요. 이 경우에는 precision과 recall 값들 간의 차이가 크기때문에 두 값을 동시에 잘 보여줄수 (상징할수) 없기 때문에 그러한 의미로 낮은 값이 도출됩니다. 두 번째 케이스는 precision과 recall을 모두 잘 대변해주고 있네요.

이렇게 precision과 recall에 대한 조화평균의 철학을 도입한 성과지표를 F1 score라고 할 수 있겠어요.

###요약하자면###

위와 같이 precision, recall에 대한 조화평균 값이 낮다고 한다면 두 가지 경우를 생각해 볼 수 있어요.

첫 번째는 precision, recall 값이 서로 차이가 많이 나는 경우입니다. 이러한 경우에는 두 값을 "동시에" 고려할만한 지표로 사용하기에 적절치 않기 때문에 조화평균값이 낮게 나옵니다. 즉, imbalance dataset 상황상에서 사용하기 힘든모델이라는 결론을 내릴 수 있어요.

두 번째는 precision, recall 값이 서로 차이가 많이 나지는 않은 경우입니다. 이러한 경우에는 precision, recall 값 모두가 낮기 때문에 이 역시 imbalance dataset 상황에서 사용하기 힘든모델이라는 결론을 내릴 수 있어요.

Precision만 너무 높아도 안되고, Recall만 너무 높아도 안되고, 이 둘 간의 평균값이 높아야 모델에 대한 전반적인 성능이 좋다고 할 수 있습니다. 그런데, 일반적인 산술평균을 적용하면 Precision or Recall 둘 중에 엄청 높은 값에 해당하는 쪽으로 평균이 치우쳐질 수 있기 때문에 조화평균을 사용하게됩니다.

일반적으로 두 값(precision, recall)이 어느정도 비례해야 좋은건데, 어느 한 값이 너무 낮아버리면 성능에도 당연히 문제가 있다고 보는게 맞기 때문에 산술평균을 쓰는것보다 조화평균을 쓰는 F1 score라는 성과지표를 사용하는것이 더 좋습니다.

[사진 래퍼런스]

사진1

http://blog.naver.com/PostView.nhn?blogId=dalsapcho&logNo=20167498252